13 Ordinary Differential Equations V

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. Solve the system
   
   $${\vec x} ' = A \vec x \qquad A = \left( \begin{array}{cc} 3 & -5 8 & -3 \end{array} \right)$$
   
   
   Neatly and accurately sketch a comprehensive set of solution curves in the $x_1,x_2$ plane. Include the eigenvectors, and/or $\vec f$, $\vec u$, and $\vec v$ in the graph if applicable. Get the slopes right.

2. Solve the system
   
   $$\dot {\vec x} = A \vec x \qquad A = \left( \begin{array}{cc} -6 & -7 7 & -20 \end{array} \right)$$
   
   
   Neatly and accurately sketch a comprehensive set of solution curves in the $x_1,x_2$ plane. Include the eigenvectors, and/or $\vec f$, $\vec u$, and $\vec v$ in the graph if applicable. Get the slopes right.

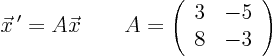
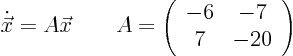
3. Please answer in order asked (even if you do the numerics first to guard against errors).

   Consider the autonomous system
   

   $$x' = x + 3y - x^2 \sin y \qquad y' = 2x + y - x y^2$$
   
   

   First analyze this system analytically:

   1. Find the critical points. One critical point is easy. Four more critical points can be found numerically. To help you a bit, their $y$-values are $\pm1.1107$ and $\pm1.6074$.
   2. Find the matrix of derivatives of vector $\vec F$ at each of the five critical point. (Actually, you can use symmetry around the origin and only find three.)
   3. Use it to analyze each critical point. List type of point and its stability.
   4. Also find the relevant eigenvectors or $\vec u$ and $\vec v$ if complex, and a $\vec f$ if defective.

4. Continuing the previous question
   1. Sketch the solution lines in the immediate vicinity of each critical point in a single $x,y$ plane. Take $-5\le x\le5$ and $-5\le y\le5$. Try to get it as accurate as possible. To do so, use the correct directions of the eigenvectors, $\vec f$, or $\vec u$ and $\vec v$.
   2. Next draw the complete exact solution plane as a dense and complete set of solution lines using a numerical solution method.

      Suitable programs to do this can be found on the web. Some I saw previously:

      http://www.math.uu.nl/people/beukers/phase/newphase.html

      http://www.scottsarra.org/applets/dirField1/dirField1.html

      http://www.math.rutgers.edu/courses/ODE/sherod/phase-local.html

      See here for Matlab software. (You will need to convert to an ODE by taking the ratio of the equations, and then the software might crash when it divides by zero if it hits a critical point.)

      You will need to use a screen grabber to make a copy that you can print. Typically you press Alt+PrintScreen or Shift-PrintScreen to get a printable copy of the active Window.

      Additional note: It has been brought to my attention that the above phase plane plotters may no longer work because the College of Engineering no longer installs Java on the web browsers. Therefore I have created a little Matlab program that does essentially the same thing. It can be found at:

      http://www.eng.famu.fsu.edu/~dommelen/courses/aim/odesols/phaseplane.m

      This program is set up to do the Van der Pol oscillator. To make it work with the system you are solving, you will need to make a few minor changes to this program, as explained in the comments at the start of the file. You will also need to create a function file myfunc.m. Pattern it after the Van der Pol example:

      http://www.eng.famu.fsu.edu/~dommelen/courses/aim/odesols/vanderpol.m

      If you use MS Notepad to create this file, do not forget to save as All Files”, not “Text Files.

      If you do not have Matlab, the free Octave clone will do just fine. You can use File/Save As in the plot window to save the plot for printing.

5. Comment on how well your predictions came out.

   State for each critical point whether critical point analysis must give the right solution near the point. In other words, could the real lines be qualitatively different from what you drew?