|
|
|
|
Next: 12 Ordinary Differential Equations IV |
|
In this class,
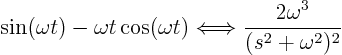
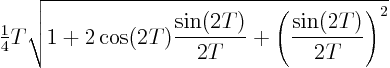
Next, check that for a resonant force ![]() with
with ![]() a constant and
a constant and ![]() , the
integrand in the
, the
integrand in the ![]() integral is always positive, so
integral is always positive, so ![]() will grow
without bound in time. However, the integrand in the
will grow
without bound in time. However, the integrand in the ![]() integral
will periodically change sign, so that
integral
will periodically change sign, so that ![]() stays finite. Address
the question why if I apply a cosine forcing, it is the
magnitude of the sine that keeps increasing instead of the
cosine. Does that make physical sense? Also verify that for
nonresonant forcing,
stays finite. Address
the question why if I apply a cosine forcing, it is the
magnitude of the sine that keeps increasing instead of the
cosine. Does that make physical sense? Also verify that for
nonresonant forcing, ![]() , both integrands
will periodically change sign, so that both
, both integrands
will periodically change sign, so that both ![]() and
and ![]() stay finite.
stay finite.