| Calculus |
|
© Leon van Dommelen |
|
1.1 Introduction
Graphs are important for engineers for a number of reasons:
- Understanding relationships between variables.
- Summarizing data.
- Representing data (like in a Moody diagram).
- Interpolating data.
- Understanding the overal nature of data. See
warming.jpg
for an example that you simply could not appreciate by looking at a
list of numbers.
- ...
Look for:

- Intercepts. Intercepts with the
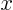 -axis satisfy
-axis satisfy 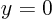 .
Intercepts with the
.
Intercepts with the 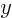 -axis satisfy
-axis satisfy 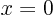 .
.

- A symmetry line exists if the curve is the same at both sides of
the line. More precisely, a symmetry line acts as a mirror that
mirrors the curve into itself. The
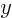 -axis is a symmetry line if
the sign of
-axis is a symmetry line if
the sign of 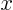 does not make a difference. The
does not make a difference. The 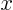 -axis is one if
the sign of
-axis is one if
the sign of 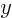 does not make a difference. The 45
does not make a difference. The 45 line
line 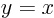 is
one if swapping
is
one if swapping 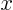 and
and 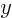 does not make a difference.
does not make a difference.

- Symmetry points. Every point on the curve must have match at
the exact opposite side of a symmetry point. Mathematically, if
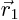 is on the curve, then so must be
is on the curve, then so must be 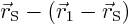 . The origin is a symmetry point
if
. The origin is a symmetry point
if  , i.e. if function
, i.e. if function 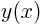 is antisymmetric.
is antisymmetric.

- Singular points:

- corners where the direction of the curve changes by an angle
less than 180
 ,
,

- cusps where it changes 180
 ,
,

- crossings where the curve crosses itself,

- positions of infinite curvature,

- ...
If 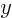 or any of its derivatives is infinite or not uniquely
defined, the curve has a singularity at that point.
or any of its derivatives is infinite or not uniquely
defined, the curve has a singularity at that point.

- A vertical asymptote
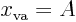 exists if
exists if 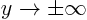 for
for 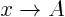 .
.

- A horizontal asymptote
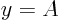 exists if
exists if 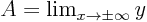 exists.
exists.

- Behavior for
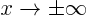 (e.g.
(e.g. 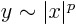 for some
for some 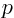 ).
).

- An oblique asymptote
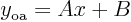 exists if
exists if
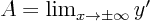 and
and 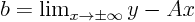 exist.
(Or more simply if
exist.
(Or more simply if 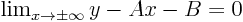 .)
.)

- Extent in
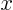 (the range of
(the range of 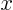 -values of the curve) and extent
in
-values of the curve) and extent
in 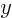 (the range of
(the range of 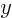 -values of the curve). If
-values of the curve). If 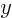 is a given
function of
is a given
function of 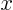 , then the
, then the 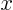 -extent is the
-extent is the 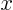 -values for which
-values for which 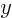 can be computed, but the
can be computed, but the 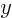 extent may not be so simple.
extent may not be so simple.

- Minima and maxima. A global maximum/minimum is the
highest/lowest value of
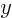 that can be found anywhere. You should
find both the value of the maximum/minimum and its location(s). A
local maximum/minimum is the highest/lowest value that can be found
in a small vicinity around the localtion of the local
maximum/minimum. Normally, you first find the local maxima/minima,
and then, based on consideration of the entire graph, decide
whether they are also global ones. The derivative changes sign at a
maximum/minimum if defined at both sides of the
maximum/minimum. So look for both zero derrivatives and singular
points.
that can be found anywhere. You should
find both the value of the maximum/minimum and its location(s). A
local maximum/minimum is the highest/lowest value that can be found
in a small vicinity around the localtion of the local
maximum/minimum. Normally, you first find the local maxima/minima,
and then, based on consideration of the entire graph, decide
whether they are also global ones. The derivative changes sign at a
maximum/minimum if defined at both sides of the
maximum/minimum. So look for both zero derrivatives and singular
points.

- Concavity is upward if
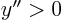 , downward if
, downward if 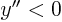 .
.

- Inflection points are points where the concavity changes sign.
See [1, Chapters 13-15]