| Calculus |
|
© Leon van Dommelen |
|
Subsections
1.2 Example
From [1, p. 128, 13a]
Asked: Draw the graph of
1.2.1 Using reasoning
Instead of starting to crunch numbers, look at the pieces first:
Factor 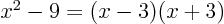 is a parabola with zeros at
is a parabola with zeros at 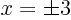 :
:
Squaring gives a quartic with double zeros at 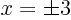 :
:
Dividing by 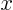 will produce a simple pole at
will produce a simple pole at 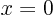 and also a sign
change at negative
and also a sign
change at negative 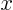 :
:
Function 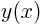 :
:

- has an
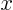 -extent
-extent 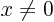 and a
and a 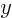 -extend
-extend 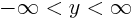 ;
;

- is odd (symmetric with respect to the origin);

- has a relative maximum at -3 of finite curvature:
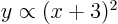 ;
;

- has a relative minimum at 3 of finite curvature:
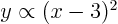 ;
;

- has a vertical asymptote at
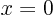 with asymptotic behavior:
with asymptotic behavior:
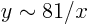 for
for 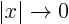 ;
;

- behaves asymptotically as
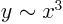 for
for 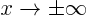 ;
;

- is concave up for
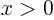 , down for
, down for 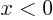 . (Should really prove
this, I guess.)
. (Should really prove
this, I guess.)
1.2.2 Using brute force
Hence

- intercepts with
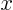 -axis are at
-axis are at 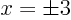 ;
;

- no intercepts with the
 axis;
axis;

 is an odd function of
is an odd function of 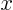 (symmetric about the origin);
(symmetric about the origin);

- for
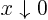 ,
, 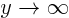 (vertical asymptote);
(vertical asymptote);

- for
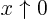 ,
, 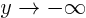 (singularity is an odd, simple pole);
(singularity is an odd, simple pole);

- for
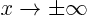 ,
, 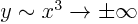 .
.
Hence,

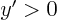 for
for 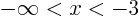 (
(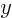 increases from
increases from 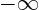 );
);

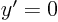 for
for 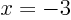 (local maximum,
(local maximum, 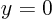 );
);

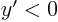 for
for 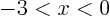 (
(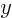 decreases towards
decreases towards 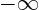 );
);

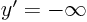 for
for 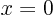 (singular point, vertical asymptote);
(singular point, vertical asymptote);

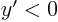 for
for 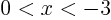 (decreases from
(decreases from 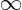 );
);

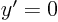 for
for 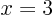 (local minimum,
(local minimum, 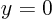 );
);

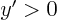 for
for 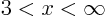 (increases to
(increases to 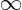 ).
).
Also,

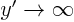 when
when 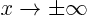 (no horizontal or oblique
asymptotes);
(no horizontal or oblique
asymptotes);

- all derivatives exist, except at
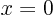 , which has no point on the curve
(no corners, cusps, infinite curvature, or other singular points);
, which has no point on the curve
(no corners, cusps, infinite curvature, or other singular points);

- probably no inflection points.
Hence

- really no inflection points (since there is no point at
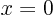 );
);

- cocave downward for
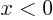 , upward for
, upward for 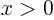 .
.
Hence the 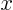 - and
- and 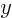 -extends are as before.
-extends are as before.
![]() is a parabola with zeros at
is a parabola with zeros at ![]() :
:
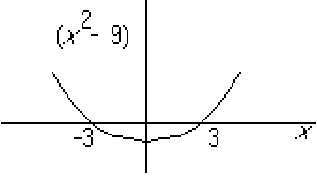
![]() :
:
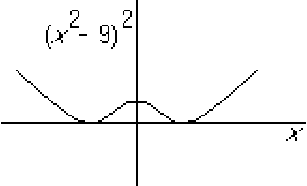
![]() will produce a simple pole at
will produce a simple pole at ![]() and also a sign
change at negative
and also a sign
change at negative ![]() :
:
![]() :
:
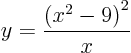
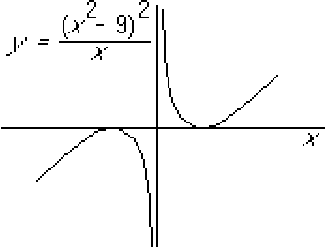
![]() - and
- and ![]() -extends are as before.
-extends are as before.