| Calculus |
|
© Leon van Dommelen |
|
Subsections
1.3 Example
From [1, p. 128, 13g]
Asked: Graph
1.3.1 Solution
Factor 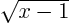 is
is 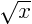 shifted one unit towards the right.
shifted one unit towards the right.
Multiplying by 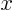 magnifies it by a factor ranging from 1 to
magnifies it by a factor ranging from 1 to 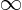 :
:
Function 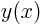 :
:
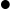
- has an
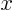 -extent
-extent 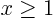 and a
and a 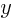 -extent
-extent 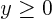 ;
;
- behaves asymptotically as
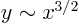 for
for 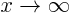 ;
;
- is monotonous:
- has vertical slope at
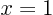 ;
;
- is concave down for smaller
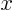 , concave up for larger
, concave up for larger 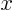 ;
;
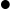
- the inflection point is at
giving 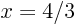 .
.
![]() is
is ![]() shifted one unit towards the right.
shifted one unit towards the right.
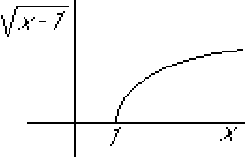
![]() magnifies it by a factor ranging from 1 to
magnifies it by a factor ranging from 1 to ![]() :
:
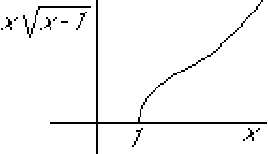
![]() :
: