3.2 Example

From [1, p. 402, 10b]

Asked: The Maclaurin series of 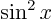$\sin^2 x$.

3.2.1 Identification

General Taylor series:

$$\begin{array}{cl} f(x) & \displaystyle = f(a) + f'(a... ...\sum_{n=0}^\infty f^{(n)}(a) \frac{(x-a)^n}{n!} \end{array}$$

This is a power series (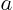$a$ is a given constant.) Maclaurin series: $a=0$.

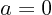Approach:

$\bullet$

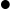
note that $a=0$;

$\bullet$

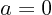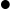
identify the derivatives;

$\bullet$

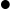
evaluate them at $a=0$;

$\bullet$

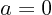put in the formula;

$\bullet$

identify the terms for any value of $n$.

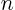3.2.2 Results

$$\begin{array}{ll} f(x) = \sin^2 x & f(0) = 0 \\ f'(x)... ... f''(x) & f^{(6)}(0) = 32 \\ \vdots & \vdots \end{array}$$

$$\begin{array}{ll} \sin^2 x & \displaystyle = f(0) + f'... ...- 8 \frac{x^4}{4!} + 32 \frac{x^6}{6!} + \ldots \end{array}$$

General expression:

$$\hbox{ When $n=2k$ with $k\ge 1$: } f^{(n)}= 2 (-4)^{ek-1} \hbox{ Otherwise: } f^{(n)}e = 0$$

$$\sin^2 x = \sum_{k=1}^\infty 2 (-4)^{k-1} \frac{x^{2k}}{(2k)!}$$

3.2.3 Other way

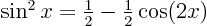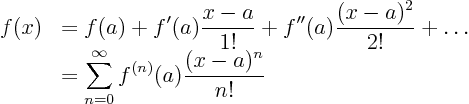
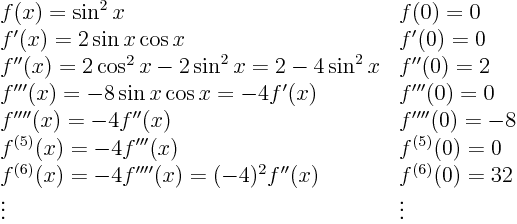
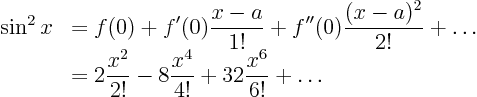
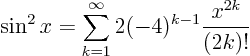
Write $\sin^2 x = \frac12 - \frac12 \cos(2x)$ and look up the Maclaurin series for the cosine. (No fair.)