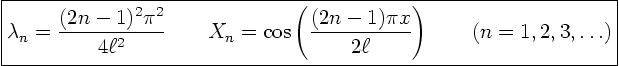|
|
|
To find the eigenfunctions ![]() , substitute a trial solution
, substitute a trial solution ![]() into the homogeneous part of the PDE,
into the homogeneous part of the PDE,
![]() . Remember: ignore the inhomogeneous part
. Remember: ignore the inhomogeneous part ![]() when finding the
eigenfunctions. Putting
when finding the
eigenfunctions. Putting ![]() into
into
![]() produces:
produces:
We then get the following Sturm-Liouville problem for any
eigenfunctions ![]() :
:
This is the exact same eigenvalue problem that we had in problem
7.28b, so I can just take the solution from there. The eigenfunctions
are: