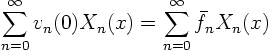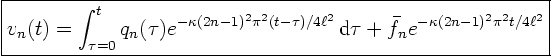| Heat conduction in a bar using separation of variables |
|
|
|
We again expand everything in the problem for  in a Fourier
series:
in a Fourier
series:
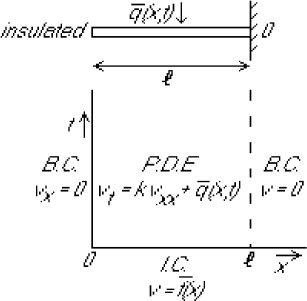
Figure 4:
Heat conduction in a bar.
 |
We write
Since 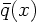 and
and 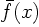 are known functions, we can find
their Fourier coefficients from orthogonality:
are known functions, we can find
their Fourier coefficients from orthogonality:
or with the eigenfunctions written out
The integrals in the bottom equal 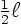 .
.
So the Fourier coefficients 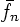 are now known constants, and the
are now known constants, and the
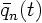 are now known functions of
are now known functions of 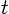 . Though in actual
application, numerical integration may be needed to find them. During
finals, I usually make the functions
. Though in actual
application, numerical integration may be needed to find them. During
finals, I usually make the functions 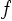 ,
, 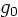 and
and 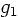 simple
enough that you can do the integrals analytically.
simple
enough that you can do the integrals analytically.
Now write the PDE
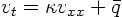 using the Fourier series:
using the Fourier series:
Looking in the previous section, the Sturm-Liouville ODE was
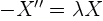 , so the PDE simplifies to:
, so the PDE simplifies to:
It will always simplify or you made a mistake.
For the sums to be equal for any 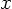 , the coefficients of every
individual eigenfunction must balance. So we get
, the coefficients of every
individual eigenfunction must balance. So we get
We have obtained an ODE for each 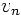 . It is again constant
coefficient, but inhomogeneous.
. It is again constant
coefficient, but inhomogeneous.
Solve the homogeneous equation first. The characteristic polynomial
is
so the homogeneous solution is
For the inhomogeneous equation, since we do not know the actual form
of the functions 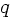 , undetermined constants is not a possibility.
So we use variation of parameter:
, undetermined constants is not a possibility.
So we use variation of parameter:
Plugging into the ODE produces
We integrate this equation to find 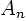 . I could write the solution
using an indefinite integral:
. I could write the solution
using an indefinite integral:
But that has the problem that the integration constant is not explicitly
shown, which makes it impossible to apply the initial condition. It is
better to write the anti-derivative using an integral with limits plus
an explicit integration constant as:
You can check using the Leibnitz rule for differentiation of integrals
(or really, just the fundamental theorem of calculus,)
that the derivative is exactly what it should be. (Also, the lower
limit does not really have to be zero; you could start the integration
from 1, if it would be simpler. The important thing is that the upper
limit is the independent variable 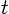 .)
.)
Putting the found solution for 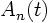 into
into
we get, cleaned up:
We still need to find the integration constant 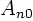 . To do so,
write the IC
. To do so,
write the IC
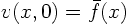 using Fourier series:
using Fourier series:
This gives us initial conditions for the 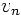 :
:
the latter from above, and hence
or writing out the eigenvalue:
We have 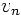 in terms of known quantities, so we are done.
in terms of known quantities, so we are done.
![]() in a Fourier
series:
in a Fourier
series:
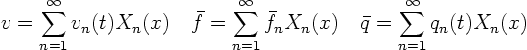
![]() and
and ![]() are known functions, we can find
their Fourier coefficients from orthogonality:
are known functions, we can find
their Fourier coefficients from orthogonality:
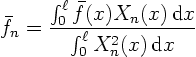
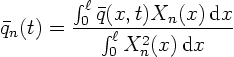
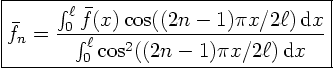
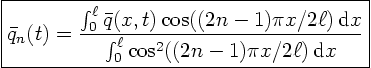
![]() are now known constants, and the
are now known constants, and the
![]() are now known functions of
are now known functions of ![]() . Though in actual
application, numerical integration may be needed to find them. During
finals, I usually make the functions
. Though in actual
application, numerical integration may be needed to find them. During
finals, I usually make the functions ![]() ,
, ![]() and
and ![]() simple
enough that you can do the integrals analytically.
simple
enough that you can do the integrals analytically.
![]() using the Fourier series:
using the Fourier series:
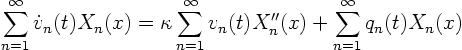
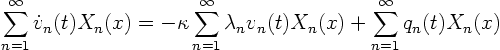
![]() , the coefficients of every
individual eigenfunction must balance. So we get
, the coefficients of every
individual eigenfunction must balance. So we get
![]() , undetermined constants is not a possibility.
So we use variation of parameter:
, undetermined constants is not a possibility.
So we use variation of parameter:
![]() into
into
![]() . To do so,
write the IC
. To do so,
write the IC
![]() using Fourier series:
using Fourier series: