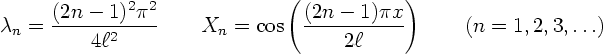|
|
|
To find the solution in the form,
Now we can take the terms depending on ![]() only to one side of the
equation, and the ones depending on
only to one side of the
equation, and the ones depending on ![]() only to the other side:
only to the other side:
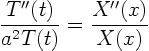
While the right hand side, ![]() , does not depend on
, does not depend on ![]() , you
would think that it would depend on the position
, you
would think that it would depend on the position ![]() ; both
; both ![]() and
and
![]() change when
change when ![]() changes. But actually,
changes. But actually, ![]() does not
change with
does not
change with ![]() ; after all, if we change
; after all, if we change ![]() , it does nothing to
, it does nothing to ![]() ,
so the left hand side does not change. And since the right hand side
is the same, it too does not change. So the right hand side does not
depend on either
,
so the left hand side does not change. And since the right hand side
is the same, it too does not change. So the right hand side does not
depend on either ![]() or
or ![]() ; it must be a constant. By convention, we
call the constant
; it must be a constant. By convention, we
call the constant ![]() :
:
If we also require ![]() to satisfy the same homogeneous boundary
conditions as
to satisfy the same homogeneous boundary
conditions as ![]() , i.e., that at
, i.e., that at ![]() , its
, its ![]() -derivative is zero,
and that at
-derivative is zero,
and that at ![]() ,
, ![]() itself is zero, we get the following problem
for
itself is zero, we get the following problem
for ![]() :
:
Note that this problem is completely homogeneous: ![]() satisfies
both the PDE and the boundary conditions. This is similar to the
eigenvalue problem for vectors
satisfies
both the PDE and the boundary conditions. This is similar to the
eigenvalue problem for vectors
![]() , which is
certainly always true when
, which is
certainly always true when ![]() . But for the eigenvalue
problem, we are interested in nonzero vectors
. But for the eigenvalue
problem, we are interested in nonzero vectors ![]() so that
so that
![]() , which only occurs for special values
, which only occurs for special values
![]() of
of ![]() .
.
Similarly, we are interested only in nonzero solutions X(x) of the above ODE and boundary conditions. Eigenvalue problems for functions such as the one above are called “Sturm-Liouville problems.” The biggest differences from matrix eigenvalue problems are:
Fortunately, the above ODE is simple: it is a constant coefficient
one, so we write its characteristic polynomial:
Case ![]() :
:
Since
![]()
We try to satisfy the boundary conditions:
Case ![]() :
:
Since ![]() we have a multiple root of the characteristic
equation, and the solution is
we have a multiple root of the characteristic
equation, and the solution is
We try to satisfy the boundary conditions again:
Case ![]() :
:
Since
![]() , the
solution of the ODE is after cleanup:
, the
solution of the ODE is after cleanup:
We try to satisfy the first boundary condition:
We now try to also satisfy the second boundary condition:
Total:
The only eigenvalues for this problem are the positive ones above, with
the corresponding eigenfunctions. If we want to evaluate them on a
computer, we need a general formula for them. You can check that it
is: