| Acoustics in a pipe using separation of variables |
|
|
|
If you look back to the beginning of the previous section, you may
wonder about the function 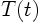 . It satisfied
. It satisfied
Now that we have found the values for 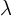 from the
from the 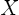 -problem,
we could solve this ODE too, and find functions
-problem,
we could solve this ODE too, and find functions
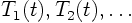 . Many people do exactly that. However, if you want to
follow the crowd, please keep in mind the following:
. Many people do exactly that. However, if you want to
follow the crowd, please keep in mind the following:
- The values of
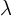 can only be found from the
Sturm-Liouville problem for
can only be found from the
Sturm-Liouville problem for 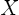 . The problem for
. The problem for 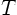 is not a
Sturm-Liouville problem and can never produce the correct
values for
is not a
Sturm-Liouville problem and can never produce the correct
values for 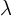 .
.
- The functions
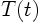 do not satisfy the same initial
conditions at time
do not satisfy the same initial
conditions at time 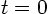 as
as 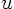 does.
does.
- Finding
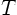 is useless if the PDE is inhomogeneous; it simply
does not work. (Unless you add still more artificial tricks to the
mix, as the book does.)
is useless if the PDE is inhomogeneous; it simply
does not work. (Unless you add still more artificial tricks to the
mix, as the book does.)
We will just ignore the entire 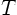 . Instead in the next section we
will systematically solve the problem for
. Instead in the next section we
will systematically solve the problem for 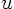 without tricks using our
found eigenfunctions. What we do there will always work. If you want
to try to take a shortcut for an homogeneous PDE, well, the
responsibility and risk are yours alone. Someday I will stop seeing
students getting themselves in major trouble this way at the final,
but it may not be this year.
without tricks using our
found eigenfunctions. What we do there will always work. If you want
to try to take a shortcut for an homogeneous PDE, well, the
responsibility and risk are yours alone. Someday I will stop seeing
students getting themselves in major trouble this way at the final,
but it may not be this year.
![]() . It satisfied
. It satisfied
![]() . Instead in the next section we
will systematically solve the problem for
. Instead in the next section we
will systematically solve the problem for ![]() without tricks using our
found eigenfunctions. What we do there will always work. If you want
to try to take a shortcut for an homogeneous PDE, well, the
responsibility and risk are yours alone. Someday I will stop seeing
students getting themselves in major trouble this way at the final,
but it may not be this year.
without tricks using our
found eigenfunctions. What we do there will always work. If you want
to try to take a shortcut for an homogeneous PDE, well, the
responsibility and risk are yours alone. Someday I will stop seeing
students getting themselves in major trouble this way at the final,
but it may not be this year.