|
|
|
So what is the procedure for solving the original problem for the
pressure ![]() having found the eigenfunctions
having found the eigenfunctions ![]() ? It is to write
everything in terms of eigenfunctions. And if I say everything, I
mean everything.
? It is to write
everything in terms of eigenfunctions. And if I say everything, I
mean everything.
We first write our solution ![]() in terms of the eigenfunctions:
in terms of the eigenfunctions:
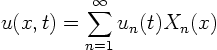
We know our eigenfunctions ![]() , but not yet our Fourier
coefficients
, but not yet our Fourier
coefficients ![]() . In fact, the
. In fact, the ![]() are what is still
missing; if we know the
are what is still
missing; if we know the ![]() , we can find the pressure
, we can find the pressure ![]() we want
by doing the sum above. On a computer probably, if we want to get
high accuracy. Or just the first few terms by hand, if we accept some
numerical error.
we want
by doing the sum above. On a computer probably, if we want to get
high accuracy. Or just the first few terms by hand, if we accept some
numerical error.
Second, we also write our PDE,
![]() , in terms of the
eigenfunctions:
, in terms of the
eigenfunctions:
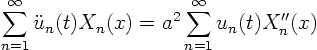
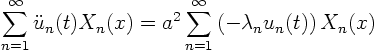
We can solve the ODE above easily. It is a constant coefficient
one, with a characteristic equation
![]() , hence
, hence
![]() , giving
, giving
So, we have already found our pressure a bit more precisely:
![\begin{displaymath}
u(x,t)= \sum_{n=1}^\infty
\left[
D_{1n} \cos\left(a \sqrt...
... +
D_{2n} \sin\left(a \sqrt\lambda_n t\right)
\right] X_n(x)
\end{displaymath}](_img78.gif)