|
|
|
In the previous section, we found the general solution of the PDE
with the given boundary conditions to be
![\begin{displaymath}
u(x,t)= \sum_{n=1}^\infty
\left[
D_{1n} \cos\left(a \sqrt...
... +
D_{2n} \sin\left(a \sqrt\lambda_n t\right)
\right] X_n(x)
\end{displaymath}](_img78.gif)
Now we want to find the coefficients ![]() and
and ![]() for
all values of
for
all values of ![]() from the initial conditions. That will fully
determine the solution.
from the initial conditions. That will fully
determine the solution.
To do so, we must first write our initial condition ![]() and
and
![]() in terms of the eigenfunctions. Writing the Fourier
series for the two functions as
in terms of the eigenfunctions. Writing the Fourier
series for the two functions as
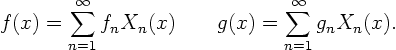
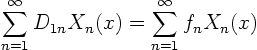
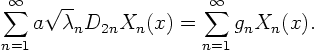
The Fourier series for ![]() becomes now
becomes now
![\begin{displaymath}
u(x,t)= \sum_{n=1}^\infty
\left[
f_n \cos\left(a \sqrt\la...
...\lambda_n} \sin\left(a \sqrt\lambda_n t\right)
\right] X_n(x)
\end{displaymath}](_img87.gif)
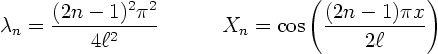
Now ![]() and
and ![]() are, supposedly, given functions, but how do we
find their Fourier coefficients? The answer is the following important
formula:
are, supposedly, given functions, but how do we
find their Fourier coefficients? The answer is the following important
formula:
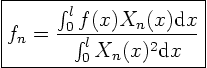
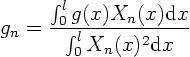
We are done! Or at least, we have done as much as we can do until
someone tells us the actual functions ![]() and
and ![]() . If they do,
we just do the integrals above to find all the
. If they do,
we just do the integrals above to find all the ![]() and
and ![]() , (maybe
analytically or on a computer), and then we can sum the expression for
, (maybe
analytically or on a computer), and then we can sum the expression for
![]() for any
for any ![]() and
and ![]() that strikes our fancy.
that strikes our fancy.
Note that we did not have to do anything with the boundary conditions
![]() and
and ![]() ; since every eigenfunction
; since every eigenfunction ![]() satisfies them, the expression for
satisfies them, the expression for ![]() above automatically also
satisfies these homogeneous boundary conditions.
above automatically also
satisfies these homogeneous boundary conditions.