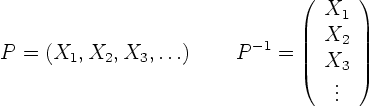|
|
|
The similarity between eigenvalue problems and Sturm-Liouville is not a coincidence. This section explores it a bit deeper:
First I want to convince you that there is no big difference between
vectors and functions. A vector ![]() is usually shown in the form
of an arrow:
is usually shown in the form
of an arrow:
However, the same vector may instead be represented as a spike diagram, by plotting the value of the components versus the component index:
In the same way as in two dimensions, a vector in three dimensions, or, for that matter, in thirty dimensions, can be represented by a spike diagram:
For a large number of dimensions, and in particular in the limit of
infinitely many dimensions, the large values of ![]() can be rescaled
into a continuous coordinate, call it
can be rescaled
into a continuous coordinate, call it ![]() . For example,
. For example, ![]() might be
defined as
might be
defined as ![]() divided by the number of dimensions. In any case, the
spike diagram becomes a function
divided by the number of dimensions. In any case, the
spike diagram becomes a function ![]() :
:
The spikes are usually not shown:
In this way, a function is just a vector in infinitely many dimensions.
The dot product of vectors is an important tool. It makes it possible to find the length of a vector, by multiplying the vector by itself and taking the square root. It is also used to check if two vectors are orthogonal: if their dot product is zero, they are. In this subsection, the dot product is defined for functions.
The usual dot product of two vectors ![]() and
and ![]() can be
found by multiplying components with the same index
can be
found by multiplying components with the same index ![]() together and
summing that:
together and
summing that:
Note the use of numeric subscripts, ![]() ,
, ![]() , and
, and ![]() rather
than
rather
than ![]() ,
, ![]() , and
, and ![]() ; it means the same thing. Numeric
subscripts allow the three term sum above to be written more compactly
as:
; it means the same thing. Numeric
subscripts allow the three term sum above to be written more compactly
as:
The dot (or “inner”) product of functions is defined in
exactly the same way as for vectors, by multiplying values at the same
![]() position together and summing. But since there are infinitely
many
position together and summing. But since there are infinitely
many ![]() -values, the sum becomes an integral:
-values, the sum becomes an integral:
| (1) |
Now let us have a look at the separation of variables procedure for
![]() . First of all, let us write this problem like
. First of all, let us write this problem like
![]() where
where ![]() is the operator
is the operator
I want to convince you that the operator ![]() is really like a matrix.
Indeed, a matrix A can transform any arbitrary vector
is really like a matrix.
Indeed, a matrix A can transform any arbitrary vector ![]() into a
different vector
into a
different vector ![]() :
:
Similarly, the operator ![]() above transforms a function into another
function,
above transforms a function into another
function, ![]() times its second order derivative:
times its second order derivative:
Now I want to convince you that the operator ![]() above is not just
a matrix, but a symmetric matrix. If a matrix
above is not just
a matrix, but a symmetric matrix. If a matrix ![]() is symmetric
then for any two vectors
is symmetric
then for any two vectors ![]() and
and ![]() ,
,
Now it is no longer that surprising that we have only real eigenvalues; that is a general property of symmetric matrices.
And remember also that symmetric matrices have orthogonal eigenvectors,
so the eigenfunctions ![]() ,
, ![]() ,
, ![]() , ...of operator
, ...of operator ![]() are going to be orthogonal. And a complete set, so we can write
any function of
are going to be orthogonal. And a complete set, so we can write
any function of ![]() in terms of these eigenfunctions, including
the initial conditions
in terms of these eigenfunctions, including
the initial conditions ![]() ,
, ![]() , and the solution
, and the solution ![]() :
:
How do we get the ![]() given
given ![]() ? Well, we usually do not
normalize the eigenfunctions to “length” one, so
the unit function in the direction of an
? Well, we usually do not
normalize the eigenfunctions to “length” one, so
the unit function in the direction of an ![]() is:
is:
Another way to understand the orthogonality relation is in terms of
transformation matrices. Note that the ![]() are just the components
of function
are just the components
of function ![]() when written in terms of the eigenfunctions. We get them
by evaluating
when written in terms of the eigenfunctions. We get them
by evaluating ![]() , where the transformation matrix
, where the transformation matrix ![]() consists
of the eigenfunctions as columns, and
consists
of the eigenfunctions as columns, and ![]() is found as the transpose
matrix (ignoring the lack of normalization of the eigenfunctions):
is found as the transpose
matrix (ignoring the lack of normalization of the eigenfunctions):