Next: 7.22, §5 Solve
Up: 7.22
Previous: 7.22, §3 Boundaries
Substitute v = T(t) X(x) into the homogeneous PDE
 :
:
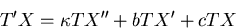
Separate:
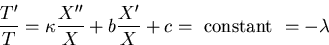
The Sturm-Liouville problem for X is now:
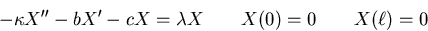
This is a constant coefficient ODE, with a characteristic polynomial:
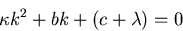
The fundamentally different cases are now two real roots (discriminant
positive), a double root (discriminant zero), and two complex conjugate
roots (discriminant negative.) We do each in turn.
Case  :
:
Roots k1 and k2 real and distinct:
X = A ek1 x + B ek2 x
Boundary conditions:
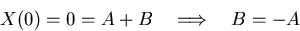
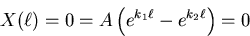
No nontrivial solutions since the roots are different.
Case 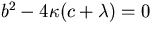 :
:
Since k1 = k2 = k:
X = A ek x + B x ek x
Boundary conditions:
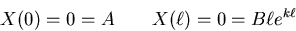
No nontrivial solutions.
Case 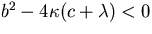 :
:
For convenience, we will write the roots of the characteristic
polynomial more concisely as:
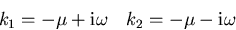
where according to the solution of the quadratic
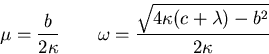
Since it can be confusing to have too many variables representing the
same thing, let's agree that 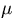 is our ``representative'' for
b, and
is our ``representative'' for
b, and 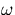 our ``representative'' for
our ``representative'' for  .In terms of these representatives, the solution is, after clean-up,
.In terms of these representatives, the solution is, after clean-up,
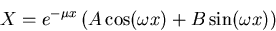
Boundary conditions:
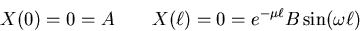
Nontrivial solutions 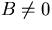 can only occur if
can only occur if
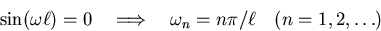
which gives us our eigenvalues, by substituting in for 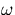 :
:
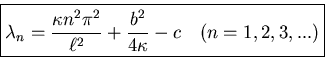
Also, choosing each B=1:
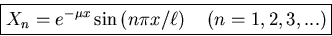
Next: 7.22, §5 Solve
Up: 7.22
Previous: 7.22, §3 Boundaries
![]() :
:
![]()
![]()
![]()
![]()
![]() :
:
![]()
![]()
![]() :
:
![]()
![]() :
:
![]()
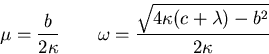
![]()
![]()
![]() can only occur if
can only occur if
![]()
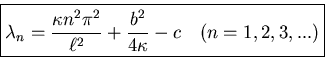
![]()