7.22, §5 Solve

Expand all variables in the problem for v in a Fourier series:

We want to first find the Fourier coefficients of the known functions and q. Unfortunately, the ODE found in the previous section,

is not in standard Sturm-Liouville form: the derivative of the first, X'', coefficient, , is zero, not -b. Let's try to make it OK by multiplying the entire equation by a factor, which will then be our .

We want that the second coefficient is the derivative of the first:

This is a simple ODE for the we are trying to find, and a valid solution is:

Having found , we can write the orthogonality relationships for the generalized Fourier coefficients of and q (remember that ):

The integrals in the bottoms equal .

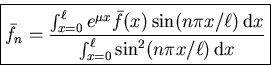
Expand the PDE in a generalized Fourier series:

Because of the choice of the X_n, :

So, the ODE for the generalized Fourier coefficients of v becomes:

Expand the IC in a generalized Fourier series:

so

Solve this O.D.E. and initial condition for v_n:

Homogeneous equation:

Inhomogeneous equation:

Initial condition: .