Next: 7.38 U, §4
Up: 7.38 U
Previous: 7.38 U, §2
Let's start trying to get rid of one variable first. We might try
a solution of the form

where the Rn would be the eigenfunctions and the 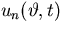 the corresponding Fourier coefficients. Unfortunately, if we try to
substitute a single term of the form
the corresponding Fourier coefficients. Unfortunately, if we try to
substitute a single term of the form 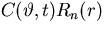 into
the homogeneous PDE, we are not able to take all r terms to the
same side of the equation and
into
the homogeneous PDE, we are not able to take all r terms to the
same side of the equation and 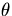 and t terms to the other side.
So we do not get a Sturm-Liouville problem for Rn.
and t terms to the other side.
So we do not get a Sturm-Liouville problem for Rn.
Try again, this time
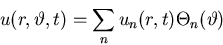
If we substitute 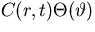 into the homogeneous PDE
into the homogeneous PDE
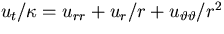 we get:
we get:
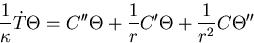
This, fortunately, can be separated:
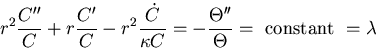
So we have a Sturm-Liouville problem for 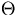 :
:
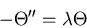
with boundary conditions that are periodic of period 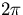 . This
problem was already fully solved in 7.38. It was the standard Fourier
series for a function of period
. This
problem was already fully solved in 7.38. It was the standard Fourier
series for a function of period 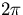 . In particular, the
eigenfunctions were
. In particular, the
eigenfunctions were 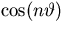 ,
, 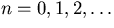 , and
, and
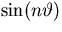 ,
, 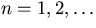 .
.
Like we did in 7.38, in order to cut down on writing, we will indicate
those eigenfunctions compactly as 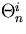 , where
, where
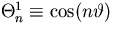 and
and 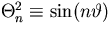 .
.
So we can concisely write
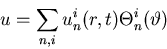
Now, if you put this into the PDE, you will see that you get rid of
the  coordinate as usual, but that still leaves you with
r and t. So instead of ODE in t, you get PDE involving both r
and t derivatives. That is not good enough.
coordinate as usual, but that still leaves you with
r and t. So instead of ODE in t, you get PDE involving both r
and t derivatives. That is not good enough.
We must go one step further: in addition we need to expand each
Fourier coefficient uin(r,t) in a generalized Fourier series in r:
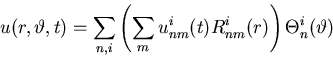
Now, if you put a single term of the form 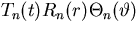 into the homogeneous PDE, you get
into the homogeneous PDE, you get
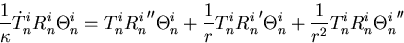
Since 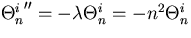 , this is
separable:
, this is
separable:
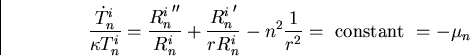
So we get a Sturm-Liouville problem for Rin with eigenvalue 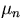
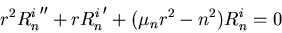
with again the same homogeneous boundary conditions as u:
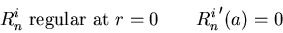
We need to find all solutions to this problem.
Unfortunately, the ODE above is not a constant coefficient one, so we
cannot write a characteristic equation. However, we have seen the
special case that 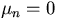 before, 7.38. It was a Euler equation.
We found in 7.38 that the only solutions that are regular at r=0
were found to be An rn. But over here, the only one of that form
that also satisfies the boundary condition Rin'=0 at r=a is the
case n=0. So, for
before, 7.38. It was a Euler equation.
We found in 7.38 that the only solutions that are regular at r=0
were found to be An rn. But over here, the only one of that form
that also satisfies the boundary condition Rin'=0 at r=a is the
case n=0. So, for 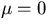 , we only get a single eigenfunction
, we only get a single eigenfunction
R00 = 1
For the case 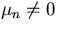 , the trick is to define a stretched r
coordinate
, the trick is to define a stretched r
coordinate 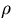 as
as
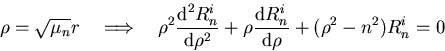
This equation can be found in any mathematical handbook in the section
on Bessel functions. It says there that solutions are the Bessel
functions of the first kind Jn and of the second kind Yn:
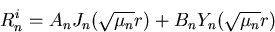
Now we need to apply the boundary conditions. Now if you look up the
graphs for the functions Yn, or their power series around the
origin, you will see that they are all singular at r=0. So,
regularity at r=0 requires Bn=0.
The boundary condition at the perimeter is
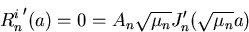
Since 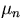 is nonzero, nontrivial solutions only occur if
is nonzero, nontrivial solutions only occur if
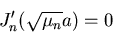
Now if you look up the graphs of the various functions J0, J1,
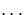 , you will see that they are all oscillatory functions, like
decaying sines, and have an infinity of maxima and minima where the
derivative is zero.
, you will see that they are all oscillatory functions, like
decaying sines, and have an infinity of maxima and minima where the
derivative is zero.
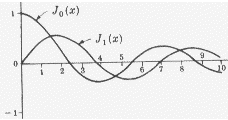
Each of the extremal points gives you a value of 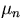 , so you will
get an infinite of values
, so you will
get an infinite of values 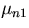 ,
, 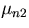 ,
, 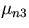 ,
,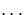 ,
, 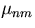 ,
, 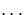 . There is no simple formula for these
values,
but you can read them off from the graph. Better still, you can find
them in tables for low values of n and m.
(Schaum's gives a table containing both the zeros of the Bessel
functions and the zeros of their derivatives.)
. There is no simple formula for these
values,
but you can read them off from the graph. Better still, you can find
them in tables for low values of n and m.
(Schaum's gives a table containing both the zeros of the Bessel
functions and the zeros of their derivatives.)
So the r-eigenvalues and eigenfunctions are:
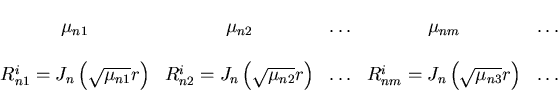
where m is the counter over the nonzero stationary points of Jn.
To include the special case 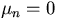 , we can simply add
, we can simply add 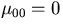 ,Ri00 = J0(0)=1 to the list above.
,Ri00 = J0(0)=1 to the list above.
In case of negative 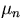 , the Bessel function Jn of imaginary
argument becomes a modified Bessel function In of real argument,
and looking at the graph of those, you see that there are no
solutions.
, the Bessel function Jn of imaginary
argument becomes a modified Bessel function In of real argument,
and looking at the graph of those, you see that there are no
solutions.
Next: 7.38 U, §4
Up: 7.38 U
Previous: 7.38 U, §2
![]()
![]()
![]()
![]()
![]() :
:
![]()
![]() , where
, where
![]() and
and ![]() .
.![]()
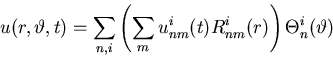
![]() into the homogeneous PDE, you get
into the homogeneous PDE, you get
![]()
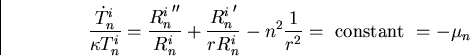
![]()
![]()
![]()
![]() before, 7.38. It was a Euler equation.
We found in 7.38 that the only solutions that are regular at r=0
were found to be An rn. But over here, the only one of that form
that also satisfies the boundary condition Rin'=0 at r=a is the
case n=0. So, for
before, 7.38. It was a Euler equation.
We found in 7.38 that the only solutions that are regular at r=0
were found to be An rn. But over here, the only one of that form
that also satisfies the boundary condition Rin'=0 at r=a is the
case n=0. So, for ![]() , we only get a single eigenfunction
, we only get a single eigenfunction
![]() , the trick is to define a stretched r
coordinate
, the trick is to define a stretched r
coordinate ![]() as
as
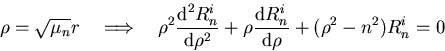
![]()
![]()
![]()

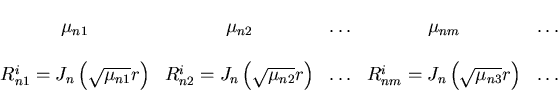
![]() , the Bessel function Jn of imaginary
argument becomes a modified Bessel function In of real argument,
and looking at the graph of those, you see that there are no
solutions.
, the Bessel function Jn of imaginary
argument becomes a modified Bessel function In of real argument,
and looking at the graph of those, you see that there are no
solutions.