7.38 U, §4 Solve

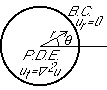
We again expand all variables in the problem in generaized Fourier series:

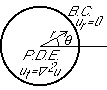
Let's start with the initial condition:

To find the Fourier coefficients fⁱ_nm, we need orthogonality for both the r and eigenfunctions. Now the ODE for the eigenfunctions was in standard form,

but the one for R_n was not:

The derivative of the first coefficient is 2r, not r. To fix it up, we must divide the equation by r. And that makes the weight factor that we need to put in the orthogonality relationship equal to r.

As a result, our orthogonality relation for the Fourier coefficients of initial condition becomes

The integral within the square brackets turns into its -Fourier coefficient fⁱ_n(r) and the outer integral turns that coefficient in its generalized r-Fourier coefficient fⁱ_nm. Note that the total numerator is an integral of f over the area of the disk against a mode shape .

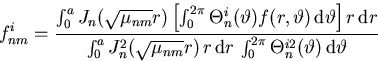
The r-integral in the denominator can be worked out using Schaum's Mathematical Handbook 24.88/27.88:

(setting the second term to zero for .)

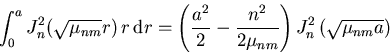
Hence, while akward, there is no fundamental problem in evaluating as many fⁱ_nm as you want numerically. We will therefor consider them now ``known''.

Next we expand the desired temperature in a generalized Fourier series:

Put into PDE :

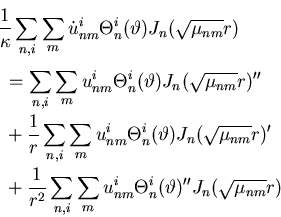
Because of the SL equation satisfied by the :

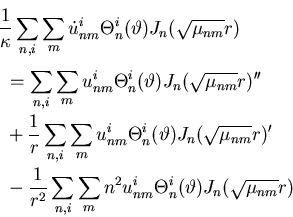
Because of the SL equation satisfied by the J_n:

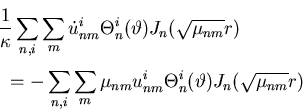
Hence the ODE for the Fourier coefficients is:

with solution:

At time zero, the series expansion for u must be the same as the one for the given initial condition f:

uⁱ_nm(0) = fⁱ_nm

Hence we have found the Fourier coefficients of u and solved the problem.