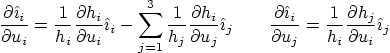4 02/06 F

1. p133, q56.

2. Derive $\vec n {\rm d}S$ in terms of ${\rm d}\theta$ and ${\rm d}\phi$, where $(r,\theta,\phi)$ are spherical coordinates, assuming that the surface is given as $r=f(\theta,\phi)$. Use that:
   
   $$\vec r = r \hat\imath_r \quad \frac{\partial \hat\imat... ...al \hat\imath_r}{\partial\phi} = \sin\theta \hat\imath_\phi$$
   
   
   as derived in class. Show that if instead the surface is given by the implicit expression $F(r,\theta,\phi)=0$, then $\partial r/\partial\theta$ and $\partial r/\partial\phi$ can be found from the total differential
   
   $$\frac{\partial F}{\partial r} {\rm d}r + \frac{\partial F}... ...m d}\theta + \frac{\partial F}{\partial\phi} {\rm d}\phi = 0$$
   
   
   Express the vector part of the final expression in terms of vector calculus.

3. p160, q38.

4. Finish finding the derivatives of the unit vectors of the spherical coordinate system using the class formulae. Then finish p160, q47 as started in class, by finding the acceleration. Note that the metric indices $h_i$ for spherical coordinates are in mathematical handbooks. Also,
   
   $$\frac{\partial {\hat \imath}_i}{\partial u_i} = \frac{1}{h... ...rac{1}{h_i} \frac{\partial h_j}{\partial u_i} {\hat \imath}_j$$
   
   

5. Express the acceleration in terms of the spherical velocity components $v_r,v_\theta,v_\phi$ and their first time derivatives, instead of derivatives of position coordinates. Like $a_r = \dot v_r + \ldots$, etc. This is how you do it in fluid mechanics, where particle position coordinates are normally not used.

6. The Laplace equation
   
   $$\mbox{PDE:}\quad u_{xx} + u_{yy} = 0$$
   
   
   where subscripts indicate derivatives, is an elliptic equation. Such a steady-state equation needs boundary conditions at all points of the boundary. For example, one properly posed problem on the unit square is
   
   $$\mbox{BC:}\quad u(x,0)=1\quad u_y(x,1)=0 \quad u(0,y)=0 \quad u_x(1,y)=0$$
   
   
   Identify 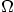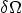$\Omega$, $\delta\Omega$, and the type of each boundary condition.

   The wave equation
   

   $$\mbox{PDE:}\quad u_{xx} - u_{yy} = 0$$
   
   
   is an hyperbolic equation. The above boundary conditions are not properly posed for the wave equation. (as you will see in a later homework.) For the wave equation, one of the coordinates must be time-like, and must have initial conditions instead of boundary conditions. The following initial and boundary conditions are properly posed for the wave equation,
   
   $$\mbox{BC and IC:}\quad u(x,0)=1\quad u_y(x,0)=0 \quad u(0,y)=0 \quad u_x(1,y)=0$$
   
   
   For each of the four, determine whether it is an IC or BC, and if so, what kind of BC. The time-like coordinate is not normally included in the domain 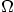$\Omega$. Under those conditions, identify 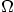$\Omega$ and $\delta\Omega$.

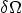   Check that the following proposed solution satisfies the PDE and all BC/IC of both the Laplace and wave equation problems:
   

   $$u = \left\{\begin{array}{l}1\mbox{ for }y<x 0\mbox{ for }y>x\end{array}\right.$$
   
   
   However, it is a valid solution to only the wave equation. Explain why it is not to the Laplace equation.

   The Laplace equation problem as written does not have a simple solution. However, if you distort the domain into a quarter circle as in
   

   $$\mbox{BC:}\quad u(x,0)=1\quad \quad u(0,y)=0 \quad \quad u_n=0\mbox{ on }x^2+y^2=1$$
   
   
   then the correct solution is simply
   
   $$u = 1 -\frac{2\theta}{\pi} \qquad \theta=\arctan(y/x)$$
   
   
   Verify that solution.