4.20. A number 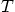 is rational if it can be written as the ratio
of a pair of integers, e.g. 1.5 = 3/2 = 6/4 = 9/6 = .... It is
irrational if it cannot, like
is rational if it can be written as the ratio
of a pair of integers, e.g. 1.5 = 3/2 = 6/4 = 9/6 = .... It is
irrational if it cannot, like 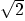 . Near any rational number,
irrational numbers can be found infinitely closely nearby, and vice
versa. For example, the value
. Near any rational number,
irrational numbers can be found infinitely closely nearby, and vice
versa. For example, the value 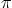 to one billion digits, as found
on the internet, is the rational number
to one billion digits, as found
on the internet, is the rational number
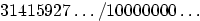 ;
; 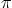 itself is not rational. The
wave equation problem when
itself is not rational. The
wave equation problem when 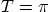 has no nonzero solutions, but
when
has no nonzero solutions, but
when 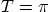 to 1 billion digits has infinitely many of them.
Obviously, in physics it is impossible to determine the final time
to infinitely many digits, so there is no physically meaningful
solution to the stated problem.
to 1 billion digits has infinitely many of them.
Obviously, in physics it is impossible to determine the final time
to infinitely many digits, so there is no physically meaningful
solution to the stated problem.
For nonzero solutions, try
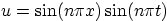 , which
satisfies the wave equation and the boundary conditions at
, which
satisfies the wave equation and the boundary conditions at 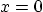 and
and
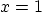 and the initial condition at
and the initial condition at 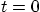 . See when it satisfies the
end condition at
. See when it satisfies the
end condition at 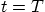 .
.
The wave equation needs two initial conditions at 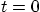 , not one
condition at
, not one
condition at 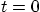 and one at
and one at 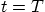 .
.
![]() , which
satisfies the wave equation and the boundary conditions at
, which
satisfies the wave equation and the boundary conditions at ![]() and
and
![]() and the initial condition at
and the initial condition at ![]() . See when it satisfies the
end condition at
. See when it satisfies the
end condition at ![]() .
.
![]() , not one
condition at
, not one
condition at ![]() and one at
and one at ![]() .
.