11 04/03 F

1. The viscous Burger's equation is:
   
   $$u_t + u u_x = \nu u_{xx}$$
   
   
   where $\nu$ is a positive constant. (This equation can be solved analytically, by setting $u=2\nu U_x$ where $e^U$ satisfies the heat equation, showing that it has smooth solutions.) Derive the conservation law for fixed intervals satisfied by the solutions of the viscous Burger's equation.

   When the viscosity is ignored as negligibly small, you get the inviscid Burger's equation:
   

   $$u_t + u u_x = 0$$
   
   
   Deduce from it, using the simplified conservation law, the speed, call it $v$, at which the conserved quantity is inviscidly propagated.

   Now the inviscid Burger's equation is a nonlinear first order equation that can have discontinuities, shocks. Derive the propagation speed, call it $a_s$, of these shocks, in terms of the quantities immediately before and behind the shock. Make use of the fact that shocks are not really discontinuities, but small regions, if small but nonzero $\nu$ is considered. And therefore the viscous Burger's equation ensures that no conserved quantity is created out of nothing nor destroyed inside the shock.

2. Continuing the previous question, in regions in the $x,t$ plane where the solution of the inviscid Burger's equation is smooth, it can be solved with the method of characteristics. Do that and write the general solution in two alternative forms, depending on which integration constant you consider to be a function of which other. Also give the propagation velocity, call it $a$, of the characteristics. Compare $a$ and $a_s$.

3. Continuing the previous question, now consider the solution due to an initial unit pulse:
   
   $$u(x,0) = \left\{ \begin{array}{l} 0 \mbox{ for } x < 0 \... ... 0 < x < 1 \\ 0 \mbox{ for } 1 < x \\ \end{array} \right.$$
   
   
   Neatly draw this initial condition in a $u,x$-plane.

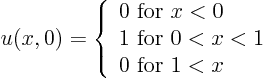
   There are two proposed solutions for $u(x,t)$ with this initial condition:
   

   $$u_1(x,t) = \left\{ \begin{array}{l} 0 \mbox{ for } x < {... ... } 1 + {\textstyle\frac{1}{2}} t < x \\ \end{array} \right.$$
   
   
   (a) Draw both solutions in $u,x$ planes at time $t=1$. (b) Draw the characteristics of both solutions in $x,t$ planes, for $t$ up to 2. (Graph or raster paper recommended.) (c) Check that both solutions satisfy the given initial condition. (d) Check that both solutions satisfy at least one of your characteristic solutions in the regions between the singularities. (e) Which one of the two solutions above is correct, if any? Why?

4. Continuing the previous question, describe what happens to solution $u_2$ when $t$ becomes larger than 2. What happens to the shock strength and velocity? Extend your earlier $x,t$ plane to include times $t>2$.

5. In 7.27, acoustics in a pipe with closed ends, assume $\ell=1$, $a=1$, $f(x)=x$, and $g(x)=1$. Graphically identify the extensions $F(x)$ and $G(x)$ of the given $f(x)$ and $g(x)$ to all $x$ that allow the solution $u$ to be written in terms of the infinite pipe D'Alembert solution.

6. Continuing the previous problem, in four separate graphs, draw $u(x,0)$, $u(x,0.25)$, $u(x,0.5)$, and $u(x,1.25)$. For all but the first graph, also include the separate terms $\frac12F(x-at)$, $\frac12F(x+at)$, and $\int_{x-at}^{x+at}G(\xi) {\rm d}\xi$. Use graph or raster paper or a plotting package. Use the D'Alembert solution only to plot, do not use a separation of variables solution in your software package. Comment on the boundary conditions. At which times are they satisfied? At which times are they not meaningful? Consider all times $0\le t<\infty$ and do not approximate.

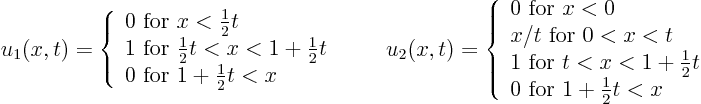
   Make sure to include your source code if any.

7. Using the D'Alembert solution of the previous problems, find $u(0.1,3)$. Be sure to show the value of each term in the expression.