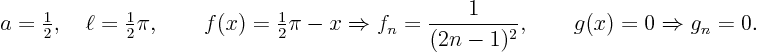(6 pts) Reconsider the separation of variables solution you
derived. Using some programming language, evaluate the found
solution at 101 equally spaced 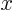 -values from 0 to
-values from 0 to 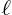 at times
0, 0.25, 0.5, and 1.25. Take
at times
0, 0.25, 0.5, and 1.25. Take 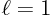 and
and 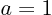 . Include at least
50 nonzero terms in the summations. Plot the solution at these four
times. Compare with the D'Alembert solution of the previous
homework, which must be the same. (Check your D'Alembert solution
first against the posted solution). Show also what happens if you
only include 10 terms in the summations.
. Include at least
50 nonzero terms in the summations. Plot the solution at these four
times. Compare with the D'Alembert solution of the previous
homework, which must be the same. (Check your D'Alembert solution
first against the posted solution). Show also what happens if you
only include 10 terms in the summations.
To help you get started, a Matlab program that plots the solution to
problem 7.28 is provided as an example. You need both
p7_28.m and p7_28u.m. This
program is valid for the PDE and BC solved in class, with the
additional data
These may of course not apply for your problem.
To run the program, enter matlab and type in p7_28. If you
do not have matlab, a free replacement is octave. Or you can use
some other programming and plotting facilities.
Include your code.