3 01/30 F

1. (6 points). 1st Ed: p78, q60, 2nd Ed: p92, q60. Also find two scalar equations that describe the line through P that crosses the surface normally at P.

   Find the unit normal $\vec n$ to the surface at P. Now assume that the surface is reflective, satisfying Snell's law. An incoming light beam parallel to the $x$-axis hits the surface at P. Find a vector equation that describes the path of the reflected beam.

   Hint: let $\vec v$ be a vector along the light ray. The component of $\vec v$ in the direction of $\vec n$ is $\vec n\cdot\vec v$. The component vector in the direction of $\vec n$ is defined as $\vec v_1=\vec n(\vec n\cdot\vec v)$. Sketch this vector along with vector $\vec n$. In which direction is the remainder $\vec v_2 =\vec v - \vec v_1$? Now figure out what happens to $\vec v_1$ and $\vec v_2$ during the reflection. Take it from there.

2. 1st Ed: p78, q62, 2nd Ed: p92, q62.

3. 1st Ed: p79, q64, 2nd Ed: p92, q64.

4. 1st Ed: p79, q70, 2nd Ed: p92, q70.

5. 1st Ed: p80, q84, 2nd Ed: p93, q84.

6. 1st Ed: p80, q87, 2nd Ed: p93, q87. (6 points) Compare with a point sink in which
   
   $$\vec v = -\frac{x{\hat\imath}+y{\hat\imath}}{x^2+y^2}$$
   
   
   Assume these are incompressible flows, in which the fluid density is constant. For each flow, compute the divergence, draw streamlines, and figure out how much fluid passes through a circle of arbitrary radius $r$. (Since the velocity is radial, the fluid flow through a circle is the magnitude of the velocity times the circumference of the circle.) Now look at a ring between two slightly different radii, and compare the fluid that goes in at one radius with the fluid that goes out at the other radius. 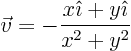Based on the results, argue that the divergence of the velocity is a measure of the source strength, the amount of fluid created out of nothing. (A sink being a negative source, where fluid disappears into nothing.) So, what do you think of the value of the divergence of the point sink at the origin (assuming that you smooth out the singularity a bit)? Note: if the fluid is not incompressible, it is really volume flows you are comparing, not mass flows, and the divergence is a measure of the relative rate of specific volume expansion. Additional volume is created out of nothing, not mass.

7. 1st Ed: p80, q102, 2nd Ed: p94, q102. Make sure that you find $\phi$ in a mathematically sound way, as discussed in class. No messing around and guessing a solution!

8. (9 points). Modified version of a question in the book. Maxwell’s equations in vacuum are
   
   $$\fbox{$\displaystyle \begin{array}{ccccc} \displaystyle ... ...a \cdot \vec E = 4 \pi \rho & \quad\emph{(d)} \end{array} $}$$
   
   
   Here $\vec E$ is the electric field, $\vec H$ the magnetic field, $\rho$ the charge density (the electric charge per unit volume), $\vec\jmath$ the current density (the current flowing per unit cross sectional area), and $c$ the speed of light, a constant. Consider $\rho$ and $\vec\jmath$ to be given functions of position and time. You need to show that any solution $\vec E,\vec H$ of the above equations is given by scalar and vector potentials $\phi,\vec A$ as described below.

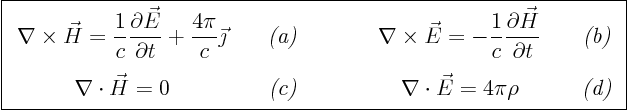
   Procedure to follow:

   1. Explain why there must be a vector potential $\vec A_0$ so that
      
      $$\vec H = \nabla \times \vec A_0$$
      
      

   2. Next define a vector $\vec E_\phi$ by setting
      
      $$\vec E = - \frac{1}{c} \frac{\partial \vec A_0}{\partial t} + \vec E_\phi$$
      
      

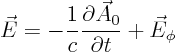
   3. Prove that the $\vec E_\phi$ defined this way is minus the gradient of some scalar potential $\phi_0$. Then the above equation becomes:
      
      $$\vec E = - \frac{1}{c} \frac{\partial\vec A_0}{\partial t} - \nabla\phi_0$$
      
      

   4. Unfortunately, $\vec A_0$ and $\phi_0$ are not unique. We now want, given potentials $\vec A_0$ and $\phi_0$, find modified potentials $\vec A$ and $\phi$. These must still give
      
      $$\fbox{$\displaystyle \vec H = \nabla \times \vec A \quad \... ...partial\vec A}{\partial t} - \nabla\phi \quad \emph{(f)} $}$$
      
      
      However, in addition they must satisfy the famous “Lorenz condition”
      
      $$\fbox{$\displaystyle \nabla\cdot\vec A + \frac{1}{c} \frac{\partial\phi}{\partial t} = 0 \quad \emph{(1)} $}$$
      
      
      (No, there is no t in Lorenz. That is another Lorentz. The Lorenz condition is critical, because it is the only condition that all observers can agree on.) The potentials you need are of the form
      
      $$\vec A = \vec A_0 + \nabla \psi \qquad \phi = \phi_0 - \frac{1}{c} \frac{\partial \psi}{\partial t}$$
      
      
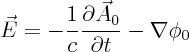
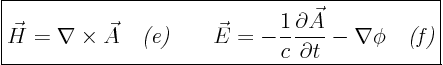
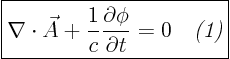
      Prove that in those terms, (e) and (f) above are true regardless of what you take for $\psi$. That is the famous gauge property of the electromagnetic field. It is central to quantum field theory. It defines the electromagnetic field in modern quantum theories, all the rest is derived.
   5. Since you can take $\psi$ whatever you like, you can choose it so that the Lorenz condition (1) is satisfied. Show that this leads to a partial differential equation for $\psi$. (This equation is called an inhomogeneous wave equation. The properties of this equation will be discussed in the second part of the class.)
   6. Now substitute what you got so far into the four Maxwell equations and so find the requirements that $\vec A$ and $\phi$ must satisfy. (I.e. get rid of the electric and magnetic fields in favor of the vector and scalar potentials $\vec A$ and $\phi$.)
   7. How come only one vector equation and one scalar equation are left?
   8. Clean up! You must obtain decoupled equations for the scalar and vector potentials.
   9. Finally, combine (a) and (d) to get a relation between the charge and current densities. (This equation is similar to the continuity equation in incompressible flow and expresses that no charge can be created out of nothing.)

9. 1st Ed: p102, q32, 2nd Ed: p122, q32. Use vector integration only.

10. 1st Ed: p103, q44, 2nd Ed: p123, q44. Use vector line integrations only.