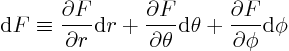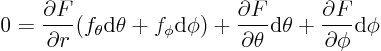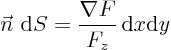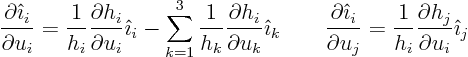Derive 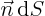 in terms of
in terms of 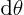 and
and 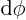 ,
where
,
where 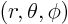 are spherical coordinates. Assume that the
surface is described as
are spherical coordinates. Assume that the
surface is described as 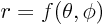 for some given function
for some given function
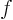 . Use the formulae given earlier in class for
. Use the formulae given earlier in class for 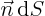 in
terms of two parameters
in
terms of two parameters 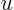 and
and 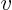 . The formula requires you to
differentiate
. The formula requires you to
differentiate 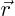 with respect to the parameters. Now in
spherical,
with respect to the parameters. Now in
spherical,
From class, the derivatives of 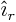 are
are
So you can now write 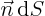 in terms of
in terms of 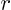 and the
derivatives
and the
derivatives 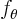 and
and 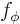 of function
of function 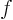 .
.
Next assume that the surface is not given as 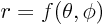 , but
as
, but
as 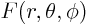 = constant. Rewrite your expression for
= constant. Rewrite your expression for
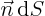 in terms of
in terms of 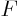 instead of
instead of 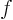 . Hint: To get the
derivatives of
. Hint: To get the
derivatives of 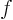 in terms of those of
in terms of those of 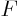 , look at the total
differential of
, look at the total
differential of 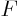 at a point on the surface:
at a point on the surface:
Now if you take 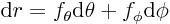 ,
you stay on the surface, so
,
you stay on the surface, so 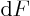 will then be zero:
will then be zero:
From this you can find 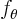 and
and 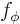 in terms of the
derivatives of
in terms of the
derivatives of 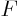 , by taking
, by taking 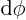 , respectively
, respectively 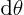 zero. Plug that into the earlier expression for
zero. Plug that into the earlier expression for 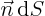 in
terms of
in
terms of 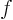 and you have
and you have 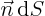 in terms of
in terms of 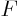 . Write
this expression in terms of the gradient of F in spherical
coordinates, as given by the expression in your notes, or in any
mathematical handbook. Compare with the Eulerian expression
. Write
this expression in terms of the gradient of F in spherical
coordinates, as given by the expression in your notes, or in any
mathematical handbook. Compare with the Eulerian expression
as derived in class. Here 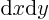 can be denoted symbolically
as
can be denoted symbolically
as 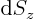 : it is the area of a surface of constant
: it is the area of a surface of constant 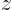 of
dimensions
of
dimensions 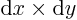 . (In other words, it is the
projection of surface element
. (In other words, it is the
projection of surface element 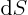 on a surface of constant
on a surface of constant 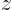 .)
What is the equivalent to
.)
What is the equivalent to 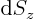 in your spherical coordinates
expression?
in your spherical coordinates
expression?
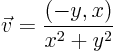
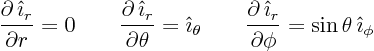
![]() , but
as
, but
as ![]() = constant. Rewrite your expression for
= constant. Rewrite your expression for
![]() in terms of
in terms of ![]() instead of
instead of ![]() . Hint: To get the
derivatives of
. Hint: To get the
derivatives of ![]() in terms of those of
in terms of those of ![]() , look at the total
differential of
, look at the total
differential of ![]() at a point on the surface:
at a point on the surface: