The domain.

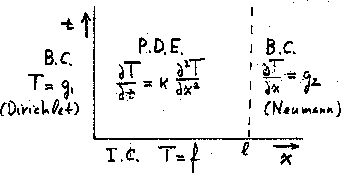
  Ordinarily, it will be required to find the temperature T for all positions x and times t of interest. In other words, the objective is not to find a single value but a function T(x,t) of two variables. The precise values of x and t that are relevant may vary; in the present case the x-values of interest range from zero to the length of the bar 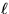$\ell$. So graphically, this restricts us to a strip in the (x,t) plane of the independent variables. Since only times past some starting time, (which we usually take to be zero), will be of interest, it restricts us further to a half strip, as shown in figure 2.

  

Figure 2: The x,t-plane for the heat equation.