12 HW 12

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. From your streamfunction solution of the previous question, find the pressure on the surface of the cylinder. Integrate the Cartesian components of the pressure force to find the lift and drag per unit span that the cylinder experiences. Disappointing results? Add an ideal vortex of strength $-\Gamma$ to the flow around the cylinder. This adds an additional velocity $-\hat\imath _\theta\Gamma/2\pi r$. (Note that this addition does not lead to violation of the boundary condition $v_r=0$ on the cylinder surface.) Find the pressure and then the lift and drag forces. You should find the D'Alembert result that the drag is zero, and the Kutta-Joukowski result that the lift is $\rho U\Gamma$ per unit span. They apply for any finite body sitting in an incoming uniform flow if the flow is ideal (no vorticity in the fluid.)

2. When the cylinder of the last question is accelerating however, D'Alembert no longer applies. The unsteady term in the potential Bernoulli law comes into play. You must be careful here, however: if you move along with the cylinder, your coordinate system is no longer an inertial one and the potential Bernoulli law as written in class does not apply. To keep it simple, assume that the cylinder is moving only along the $x$-axis of a true inertial coordinate system. Take its center point position $x_0$ to be some arbitrary function of time $x=x_0(t)$. Moving along with the cylinder, the fluid at infinity seems to move in the negative $x$-direction with speed $-\dot x_0$. So the complex velocity potential that you see when moving along with the cylinder is
   
   $$F' = - \dot x_0 \left(z' + \frac{a^2}{z'}\right) \qquad z' = z - x_0 = (x-x_0) + {\rm i}y$$
   
   
   Here $a$ is the radius of the cylinder and primes denote quantities perceived by someone moving along with the cylinder. But we need the flow in the inertial system to find the pressure. The $-\dot x_0 z'$ term is the apparent uniform flow velocity caused by the motion of the observer. An observer in the inertial coordinate system does not observe this term; the fluid at infinity is at rest compared to this observer, so in the inertial system
   
   $$F = - \dot x_0 \frac{a^2}{z'}$$
   
   
   Noting that ${\rm d}/{\rm d}z$, keeping time constant, is the same as ${\rm d}/{\rm d}z'$, show then that for an inertial observer
   
   $$W = \dot x_0\frac{a^2}{(x-x_0+iy)^2} \qquad \phi = -\dot x_0 \frac{a^2(x-x_0)}{(x-x_0)^2+y^2}$$
   
   
   the latter from first multiplying top and bottom of $F$ with $\bar z'$. Now find the pressure. The expression for $W$ allows you to find the kinetic energy. When differentiating $\phi$ with respect to time, make sure to differentiate every $x_0$ and $\dot x_0$, not just half of them. Next evaluate the pressure in particular on the surface, by noting that on the surface
   
   $$x-x_0 = a \cos \theta' \qquad y = a \sin \theta'$$
   
   
   There should be one additional term that you did not have for the nonaccelerating cylinder. Show that it produces an additional pressure force
   
   $$F_x = - \rho\pi a^2 \ddot x_0$$
   
   
   To balance this force of the fluid on the cylinder, you will have to exert the opposite force. So the force above represents a drag $D$. Of course, if the cylinder has mass $m$ per unit span, to give it acceleration $\ddot x_0$ you also have to apply a force $F_x=m \ddot x_0$. The total force you must exert is therefore
   
   $$F_x = (m + \rho\pi a^2) \ddot x_0$$
   
   
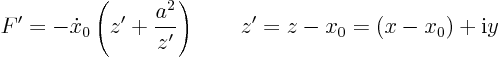
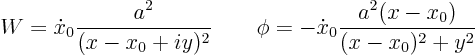
   So apparently the surrounding fluid exerts an additional force on the cylinder that acts as if you have to accelerate an additional mass $\rho\pi a^2$. This additional mass is called the added mass” or “apparent mass. It expresses the fact that in accelerating the cylinder, you must also do work to add kinetic energy to the fluid in its vicinity. For a circular cylinder, the apparent mass happens to be exactly that of a cylinder of fluid of that radius. In general however, the apparent mass is different from that of a body of fluid of the same shape.

3. Reconsider the two trailing vortices above the ground of the previous homework. In this case however, write down the total complex potential due to the four vortices first. Note: to find a source sitting at $z_0$ instead of at the origin, replace $z$ by $z-z_0$. For one vortex, $z_0$ might be $\ell+{\rm i}h$. Differentiate the total potential with respect to $z$ to find the total $W$. From that find the pressure using complex conjugates. Check that you get the same pressure as before. Also find the streamfunction of one vortex and its mirror. Evaluate at the ground, where $z=x$, and then show that the streamfunction is a constant, zero, at the ground as it should. Note, for any complex number $a=a_r+{\rm i}a_i=\vert a\vert e^{{\rm i}\alpha}$, where $a_r$, $a_i$, and $\alpha$ are complex numbers,
   
   $$\ln(a) = \ln(\vert a\vert)+ {\rm i}\alpha \qquad \vert a\vert=\sqrt{a_r^2+a_i^2} \qquad \alpha=\arctan(a_i/a_r)$$
   
   
   If $a$ is a ratio $b/c$=$\vert b\vert e^{{\rm i}\beta}/\vert c\vert e^{{\rm i}\gamma}$, note that $\vert a\vert=\vert b\vert/\vert c\vert$ and $\alpha=\beta-\gamma$.

4. Consider a wall that for $x>0$ is along the $x$-axis. A fluid is flowing in the minus $x$-direction along this wall. At the origin however, the wall bends upwards by 30 degrees, producing an inside corner of 150 degrees. Find the expression for the complex velocity potential of this flow. To find the sign of the constant, find the velocity at a single, easy point, and check its sign. As noted, the flow must be going in the negative $x$-direction. Find the streamfunction and from that, sketch the streamlines. Find the velocity, and so show that the corner point is a stagnation point. Find the wall pressure and sketch its distribution with $x$. In a real viscous flow at high Reynolds number, a thin boundary layer along the wall upstream of the corner will be unable to withstand much of the adverse pressure gradient slowing it down. So the boundary layer will separate before it reaches the corner, and reattach to the wall downstream of it. Based on that, sketch how you think the viscous streamlines will look like.

   Next assume that at the origin the wall bends downwards by 30 degrees, producing a 210 degree corner. Repeat the analysis and sketching. In this case you should find that there is infinitely large negative pressure at the corner. The boundary layer approaching the corner now finds things plain sailing until it reaches the corner. But right at the corner it is not going to go around it, as that would produce a very strong adverse pressure gradient. Instead the boundary layer just keeps going straight along the $x$-axis immediately behind the corner. That effectively eliminates the corner and its associated pressure gradient. This effect is why flows around airfoils with sharp trailing edges and sufficiently blunted leading edges satisfy the Kutta-Joukowski condition.

   Finally, if the flow is unsteady (i.e. if the constant in your complex potential varies with time), how does that affect whether the ideal flow at the corner has stagnation or infinitely negative pressure?