13 HW 13

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. Consider the combination of a uniform flow of velocity $U$ in the $x$-direction with a source of strength $q$ (volumetric flow rate per unit span) at the origin. (a) Find the complex conjugate velocity $W$ and from that the stagnation point(s). (b) Find the equation for the streamline(s) passing through the stagnation point(s). Draw this and other streamlines. (c) If you solidify (replace by a solid material) the fluid coming out of the sink, you get the flow around a solid body. Shade this solid body in your graph. (d) What is the maximum cross sectional (in the $y$-direction) area of the body?

2. Write down the complex velocity potential for flow around a cylinder of radius 2 in a complex $\zeta$ plane if the velocity at infinity is $U\hat\imath$. What is the maximum velocity on the surface of the cylinder? Then use the Joukowski transformation to map the circle to an ellipse in a complex $z$-plane. What is the aspect ratio of the ellipse? What is the maximum velocity on the surface of the ellipse? (Use the chain rule of differentiation to find $W$.) What is the pressure coefficient $C_p=(p-p_\infty)/\frac12\rho{U}^2$ at that point?

3. Write down the complex velocity potential for the combination of (a) a uniform flow of magnitude $U$ in the positive $x$-direction, (b) a source of strength $q=C/\varepsilon$ at the origin, (c) a sink (negative source) of strength $q=C/\varepsilon$ at $z=\varepsilon$. Show that in the limit $\varepsilon\to 0$, you get the potential flow around a cylinder. Find the radius of that cylinder.

4. Consider the complex velocity potential
   
   $$F = U\left(\zeta_0+\frac{r_0^2}{\zeta_0}\right) + \frac{{\rm i}\Gamma}{2\pi} \ln \frac{\zeta_0}{r_0}$$
   
   
   where $U$, $r_0$, and $\Gamma$ are real positive constants. (a) What sort of flow is this? Sketch the streamlines for $\Gamma=0$, $0<\Gamma<4\pi r_0 U$, and $4\pi r_0 U<\Gamma$ in separate complex $\zeta_0$ planes. (b) Consider the conformal transformation $\zeta=\zeta_0e^{{\rm i}\alpha}$. What does this transformation do? In particular sketch the streamlines of velocity potential $F$ in separate complex $\zeta$ planes for $\alpha$, say, 0.25 radians (about 15 degrees). (c) Find the value of $\Gamma$ for which the complex conjugate velocity $W$ at the trailing edge $\zeta=r_0$ is zero. (Rewrite $F$ first in terms of $\zeta$.) (d) What is the lift per unit length $l$ of the cylinder for this circulation? (e) Assume now that $r_0=1$. In that case, the Joukowski transformation $z=\zeta+1/\zeta$ maps the cylinder into a flat plate airfoil. Show that the lift coefficient
   
   $$c_l = \frac{l}{\frac12\rho U^2 c} = 2\pi \sin\alpha$$
   
   
   for that airfoil, if $c$ is the chord, i.e. the distance between trailing edge and leading edge of the flat plate in the $z$-plane.

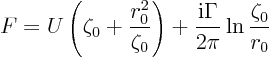
5. Continuing the previous question, if we want a Joukowski airfoil instead of a flat plate, we can make the radius $r_0$ slightly bigger than 1. In that case, the trailing edge is of course no longer at $\zeta=1$, but at $\zeta=r_0$. Then the usual Joukowski transformation no longer works correctly to produce a sharp trailing edge. But we can fix this by shifting the transformation by an amount $s$ equal to the shift in trailing edge:
   
   $$z = \zeta-s + \frac{1}{\zeta-s} \quad \mbox{where}\quad s=r_0-1$$
   
   
   Noting this, download the matlab program airfoil.m and read through it. Now use the program to make a nice picture of the streamlines around a cambered Joukowski airfoil at an angle of attack. Note: you may want to make use of an undocumented feature of the program. Explain what that feature is.

6. (a) Sketch the Joukowski airfoil of the previous question and then sketch and describe the boundary layer coordinates and velocity components that you would use in finding the boundary layer solution around the airfoil. (Do so at a nontrivial arbitrary point in the boundary layer to make the features clear.) (b) Do the same for the boundary layer around the ellipse, taking as the boundary layer starting point the front (upstream) stagnation point. What are the boundary conditions at the wall? What is the initial condition for $u(0,y)$ at the start of the boundary layer? 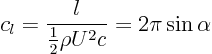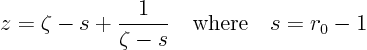What is the boundary condition for the boundary layer $u$ when $y/\sqrt{\nu}$ becomes infinite at the top point of the ellipse? Suppose that the circle in the complex $\zeta$-plane is given as $\zeta=2 e^{{\rm i}\phi}$. Then for any arbitrary $\phi$, at the corresponding $x$-position on the ellipse, what is the boundary condition for the boundary layer velocity component $u$ when $y/\sqrt{\nu}$ becomes infinite?

7. The Blasius solutions puts a semi-infinite plate along the positive $x$-axis in a uniform flow in the $x$-direction. Then it finds the boundary layer that develops at large Reynolds numbers along that plate. But consider the flow towards a sink at the origin of strength $q=2\pi s$:
   
   $$F = - s \ln z$$
   
   
   We can put a semi-infinite plate along the positive $x$-axis in that flow instead. Find the boundary layer solution for that flow. In particular, first find the potential flow velocity on the surface of the plate. Then write the boundary layer equations. Write out the boundary condition $u\to u_e$ when $y/\sqrt{\nu}$ becomes infinite; in particular identify $u_e$. Now use dimensional analysis to find the form of the solution, noting that $s$, not some $U$, is the given constant in this problem. Put the obtained streamfunction expression in the boundary layer equations. Note, you may want to include a minus sign in your expression for the streamfunction, since the flow is now in the negative $x$-direction. Do not forget that unlike for Blasius, $\partial p/\partial x$ is not zero in this case.

   (The obtained differential equation can be solved analytically without a computer, a rarity in boundary layer theory. Can you do this for extra credit? The key step is to define new variables $\alpha=f'$ and $\phi=f''$ and then write an equation for ${\rm d}\phi/{\rm d}\alpha$ in terms of $\alpha$ and $\phi$, noting that $f'''={\rm d}f''/{\rm d}\eta = ({\rm d}f''/{\rm d}f')({\rm d}f'/{\rm d}\eta$.)

8. According to potential flow theory, what would be the lift per unit span of a flat-plate airfoil of chord 2 m moving at 30 m/s at sea level at an angle of attack of 10 degrees? What would be the viscous drag if you compute it as if the airfoil is a flat plate aligned with the flow with that chord and the flow is laminar? Only include the shear stress over the last 98% of the chord, since near the leading edge the shear stress will be much different from an aligned flat plate. What is the lift to drag ratio? Comment on the value. Use $\rho=1.225$ kg/m$^3$ and $\nu=14.5\;10^{-6}$ m$^2$/s.

9. Assume that a flow enters a two dimensional duct of constant area. If no boundary layers developed along the wall, the centerline velocity of the flow would stay constant. Assuming that a Blasius boundary layer develops along each wall, what is the correct expression for the centerline velocity in the entrance part of the duct?

10. Continuing the previous question. Approximate the Blasius velocity profile to be parabolic up to $\eta=3$, and constant from there on. Sketch the duct, including the lines that correspond to $\eta=3$ and the lines that correspond to the displacement thickness. At what point along the duct would you estimate that developed flow starts based on the parabolic approximation? Sketch the velocity profile at this point, as well as at the start of the duct, and at the point of the duct where the range $0\le\eta\le3$ corresponds to $\frac18$ of the duct height accurately in a single graph. Remember the previous question while doing this!