Most of the time in fluids, we want the time changes for fixed control volumes (FCV):
![]()
Trick: find out what happens to MFCV from what happens to the mass of the material region that coincides with the control volume at whatever time t you are interested in. You know what happens to the mass of that material region (it remains constant).
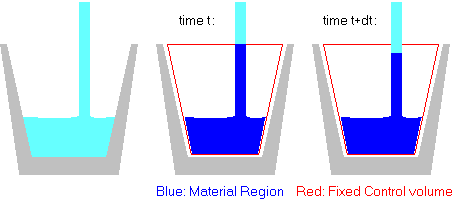
Now use mathematics to rewrite the time derivative of the material region in terms of the time derivative of the fixed control volume. They are not the same. In the picture above, the material region keeps the same mass, while the control volume mass grows. If you do the math right, (see below for details), what you will find is that
![]()
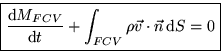 |
(2) |
In words, the boxed formula says: The rate of increase in mass of the control volume plus the rate of mass flowing out of the control volume add to zero. The mass flowing out is the surface integral. It is the outflow correction to the physical law for a fixed region.
Look a bit closer at the integral. Outflow corrections are always an
integral over the outside surface area S of the volume (which would
include the top plane through the rim of the glass, if that is our
control volume.) In the integrand, ![]() is of course the flow
velocity, while
is of course the flow
velocity, while ![]() is the unit vector normal to the boundary.
(For the the top plane through the rim of the glass, that would be a
vector of unit length sticking upwards.) So
is the unit vector normal to the boundary.
(For the the top plane through the rim of the glass, that would be a
vector of unit length sticking upwards.) So ![]() is
the component of the velocity normal to the boundary (and
positive outward.) It gives the speed of outflow through the
boundary. Speed, area and density all increase the mass flow through
the boundary.
is
the component of the velocity normal to the boundary (and
positive outward.) It gives the speed of outflow through the
boundary. Speed, area and density all increase the mass flow through
the boundary.
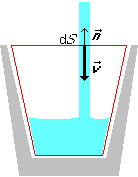
In the picture above, the surface integral is over the entire red
outside area of the fixed control volume. But almost all of it is
zero. Either the density is zero (no water), or the velocity ![]() normal to the boundary is zero. The only part of the
integral that is nonzero is where the water stream cuts through the
red control volume surface. If the cross-sectional area of the stream
is
normal to the boundary is zero. The only part of the
integral that is nonzero is where the water stream cuts through the
red control volume surface. If the cross-sectional area of the stream
is ![]() and the velocity has magnitude Vs downward, then
and the velocity has magnitude Vs downward, then
![]() . So in this
example, mass conservation for the glass says
. So in this
example, mass conservation for the glass says
![]()
Bottom line: if you start applying physical laws to fixed spatial regions instead of to material regions, you better be adding outflow corrections. These outflow corrections are always integrals over the outside surface of the control volume.
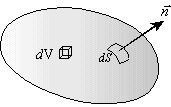
Note that the mass itself is an integral over the interior volume;
![]() . Conserved properties like mass are found from
integrals over the interior, while outflow corrections are integrals
over the boundary.
. Conserved properties like mass are found from
integrals over the interior, while outflow corrections are integrals
over the boundary.
We did not yet actually derive the above formula. To do so, we must
recognize that the time derivative that we know is the time derivative
of the mass of the material region. That means we must differentiate
an integral ![]() over a region with moving boundaries.
Such derivatives can be found using the Leibnitz rule.
over a region with moving boundaries.
Such derivatives can be found using the Leibnitz rule.
![]()
![]()
If we apply this to the integral of the mass of the material region
![]() , we get:
, we get:
![]()
![]()
Exercise:
Evaluateif
,
, and V is the unit cube
.
Instead of using the Leibnitz rule, we can derive the mass equation for a fixed control volume from more physical arguments. This is done on the class web page under Reynolds Transport Theorem.
You should now be able to do questions 5.5 and 5.1 (minus some physical interpretations.)