Integral forms of laws like the one just derived for mass conservation are very useful if you want to know the overall properties of a system (its mass, the total force produced by an engine, etcetera.) But if you want to find the detailed properties of a flow at all points, you need Partial Differential Equations (PDEs) that apply at every point. You can find these from the integral form by looking at very small regions.
Here, we want to convert the integral mass conservation equation for a fixed control volume,
![]()
![]()
The divergence theorem takes surface integrals to volume integrals and vice-versa.
![]()
![]()
Apply this to mass conservation (with ![]() ),
),
![]()
![]()
So the PDE form of the continuity equation is:
| (3) |
Index notation (with Einstein summation convention):
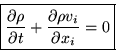 |
(4) |
Note that in the above equation, each term is simply the derivative of something. An equation that looks like that is called an equation in conservation form. It comes directly from a conservation law (here mass conservation) and can directly be turned back into a conservation law by integrating it over a volume.
But if we start differentiating out the individual factors, we get a nonconservative form:
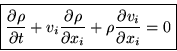 |
(5) |
But nonconservative forms can be more accurate under other circumstances. Also, they often show important aspects of the physics. For example, the terms in the nonconservative continuity equation can be rewritten as (remember the Lagrangian total derivative):
![]()
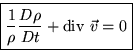 |
(6) |
As an important special case, for incompressible fluids:
| (7) |
You should now be able to do question 5.2