Example

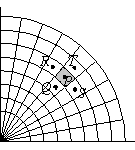
Problem: We want to do a computation of a fluid flow in two dimensions. We will use polar coordinates. We chop the flow region up into small volumes and now we must derive equations for each of those small volumes. Write an approximate continuity equation for the shaded volume in terms of the densities and polar velocity components at points P, Q, R, S, and T.

Solution: Let us choose the flow quantities at the centers of all the small volumes as the unknowns. We want to write equations for these unknowns. We start with the derived integral mass conservation equation for a fixed region:

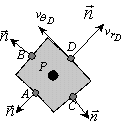
We apply this to the shaded region. We will make approximations to express the two terms in terms of the density at only a finite number of points:

Finally we can get rid of the side points A, B, C, and D by approximating further, eg, .There may be further considerations, see Intro to Computational Mechanics.

Exercise:

Derive the continuity partial differential equation in polar coordinates by taking the limit . (See the appendices in the book for this equation in various coordinate systems.)

In the homework, you will do all this in spherical coordinates, i.e. derive both the equation for a finite volume and the PDE. The mathematical handbook has a couple of different pictures of spherical coordinates; many calculus books have a picture of a volume .