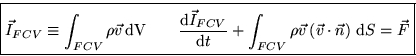Next: PDE conversion
Up: Momentum Conservation
Previous: Momentum Conservation
For practical reasons, we would again like to convert the momentum
equation into one for a fixed control volume.
To do this, we again use the Leibnitz rule on the components of the
momentum equation for the material region that instantaneously
coincides with the fixed control volume:
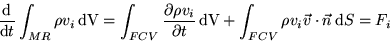
Hence, for the same reasons as for the continuity equation,
| 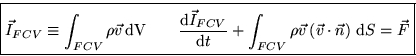 |
(10) |
Again, we get a surface integral as an outflow correction in addition
to what we have in physics. Note the additional 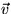 in this
integral compared to the continuity integral: we are now integrating
momentum flowing out, not mass flowing out.
in this
integral compared to the continuity integral: we are now integrating
momentum flowing out, not mass flowing out.
You should now be able to do questions 5.1, 5.11, 5.12, 5.13, 5.14
Next: PDE conversion
Up: Momentum Conservation
Previous: Momentum Conservation
![]()