(Book: 5.7)
Next, we will convert the momentum equation into a PDE as a tool to eventually find detailed solutions of flow fields. The momentum equations for inviscid flow in PDE form are called the Euler equations. The momentum equations for viscous flow in PDE form are called the Navier-Stokes equations.
We start with the derived integral momentum equation,
![]()
![]()
![]()
So, the conservation PDE form of the momentum equations is:
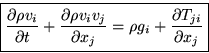 |
(11) |
To get the also useful nonconservative form, we can again differentiate out:
![]()
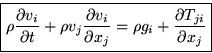 |
(12) |
We can again make this more physical by recognizing the Lagrangian derivative of the velocity in it:
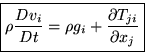 |
(13) |
Exercise:
Derive the corresponding Euler equation by restricting the total stress Tij. Write the equation in vector form. Explain by a simple example that the pressure does not give you the net force per unit volume on the fluid, but that you need the pressure gradient.
You should now be able to do questions 5.4, 5.6