Contour Integrals

We will look a bit at contour integrals of arbitrary complex functions f. Your first idea should be that a contour integral of a complex function, would be zero. After all, assuming the antiderivative of f exists, call it F, the integral would be the difference between F at start and end of integration. For a closed contour, start and end are the same.

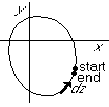
As an example,

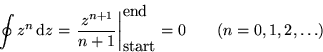
However, the integral is not always zero. F might be multiple-valued: in that case, we might need a different value for F at the end than at the beginning. For example, for any contour that goes once around the origin:

While r and hence returns to the same value at the end, will have increased by an amount , making the integral equal to .

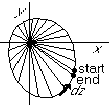
Note that function f=1/z is singular at z=0. As this example shows, the value of a complex contour integral depends critically on singularities inside the contour:

As a consequence:

In the figure, the integral around contour C₁ is the same as around contour C₂ as long as there are no singularities inside the grey area:

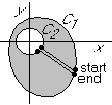
Exercise:

Integrate along a circle of unit radius around the origin z=0. Hint: contract the circle to a very small circle around the origin and then approximate.

You should now be able to do The exercise above.