Far Field

Consider a two-dimensional body that moves through an irrotational, incompressible fluid. The fluid is at rest at large distances from the body.

Exercise:

Show that the circulation around the body is given by , where F is the complex velocity potential.

Since is a complex contour integral, we can push the contour of integration for way out into the far field.

Exercise:

For the same case, show that the volumetric flow rate through a fixed contour around the body is given by , where F is the complex velocity potential. Why will this integral ordinarily be zero?

At large distances from the body, the complex conjugate velocity behaves as:

After all, if we had logarithmic factors or broken powers, the velocity would not be unique. From W we find

Note that the first term is in general a combination of a source (C real) and a vortex (C purely imaginary.)

Because the circulation and volumetric flow rate must still be the same at large distances

where m is the volumetric expansion rate of the body (zero for a solid body).

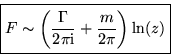
It follows that at large distances, a two-dimensional airfoil looks like a point vortex.

You should now be able to do The exercises above.