Laws

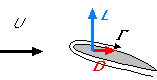
The aerodynamic forces on a body moving at constant velocity are the drag force D opposing the motion and the lift force L in the direction normal to the motion.

For unseparated incompressible potential flow past a two-dimensional body around which there is a circulation :

D'Alembert's Paradox:

According to D'Alembert, no energy is needed to overcome drag!

Kutta-Joukowski:

According to this, we can get nonzero lift without doing any work.

Proof of the laws: we saw before that at large distances, the velocity potential induced by the body approaches a vortex flow. So for large z:

Doing Blasius' integral along a very large circle around the body,

Note that the circulation must be clockwise (increase the velocity above the airfoil) to produce upward lift.

Exercise:

Approximate the airfoil as a thin flat plate 0<x<c where c is the cord length. Assume that the slip velocity above the plate is U+u_u(x) and on the bottom U+u_b(x) where U is the constant speed of flight. Use the Bernoulli law to find the pressures on the surface and then approximate for small u_u and u_b. Show that the Kutta-Joukowski value of the lift is obtained.

You should now be able to do The exercise above.