Mirror method

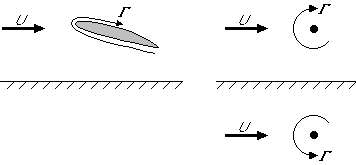
Given a two-dimensional airfoil . We want to approximate the effect of having a ground below the airfoil as compared to the airfoil in free space. To do so, we ``mirror'' the entire flow field into the ground. Then the ground is a streamline because of symmetry. It is really good enough to approximate the airfoil by a vortex while doing this:

By symmetry, the ground is now a streamline. The method of accounting for walls by mirroring the flow field into the wall is called the mirror method.

Exercise:

Write the combined potential of the two vortices and the uniform stream, and so verify that the ground is indeed a streamline.

It follows that the effect of the ground is the same as that of adding a mirror vortex below the ground. Near the airfoil, the effect of the second vortex (hence of the ground) is to decrease the effective wind velocity.

For three-dimensional wings, another effect of the mirror vortices is to reduce the induced drag caused by the trailing vortices.

You should now be able to do 18.7, 19, 21