For incompressible potential flows, the three momentum equations can be replaced by a single ``potential flow Bernoulli equation.''
The momentum equations for [in]viscid potential flow are:
![]()
Potential Flow Bernoulli equation:
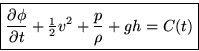
Exercise:
Answer the following questions:
- How did I get this?
- Does this require points to be along the same streamline?
- Does this require the flow to be steady?
- Does this require the fluid to be inviscid?
- So how come there are viscous incompressible potential flows?
- Does this require the flow to be incompressible?
- How about compressible isentropic flows?
- Does the compressible isentropic flow have to be inviscid?
Exercise:
Draw the isobars for ideal stagnation point flow (u,v)= a(x,-y).
Bottom line: to find incompressible potential flow, solve
![]()