Complex variables

Complex variables are very powerful in dealing with 2D irrotational incompressible flows.

Define:

then cannot be found anywhere on the real axis. This allows us to ``pack'' two real numbers into one complex number, eg:

Here z is the complex position coordinate,

F is the complex velocity potential, and W is the complex conjugate (because of the - sign) velocity.

What we have achieved is to replace the two dimensional vectors (x,y), , and (u,v) by scalar (complex) numbers.

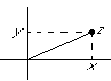
I can get the components of a given position z by writing z in the form where x and y are real. In that case, x is the x-component, and y is the y-component of the position z. We write (the real part of z) and (the imaginary part of z, i.e. the real number multiplying .)

Exercise:

If z=(1+i)+i(2+i), what are x and y?

Complex numbers have the same general properties as ordinary numbers, except that they cannot be ordered (no >, <).

Exercise:

What are W and F for ideal stagnation point flow (u,v)= a(x,-y)? (Express in terms of z.)