Next: Some Manipulations
Up: Introduction
Previous: Complex variables
Any differentiable complex function F(z) is the complex
potential for a 2D incompressible potential flow. Further  is the complex conjugate velocity.
is the complex conjugate velocity.
Reason: differentiability requires that 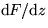 is the same
whichever direction we take
is the same
whichever direction we take 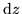 . In particular if we take
. In particular if we take 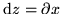 , a change in x only, we should get the same as
when we take
, a change in x only, we should get the same as
when we take 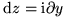 , a change in y only.
That means, if
, a change in y only.
That means, if 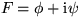 :
:
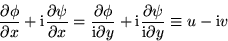
Since  ,
,
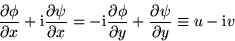
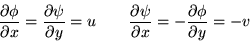
from which it follows that u and v satisfy both the continuity
equation and irrotationality:
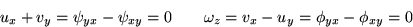
Differentiable complex functions are easy to find:
- Constants are differentiable:
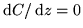 .
. - Function F(z)=z is differentiable:
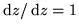 .
. - Sums of differentiable functions are differentiable (see your calculus
book.)
- Products of differentiable functions are differentiable (see
your calculus book.)
- Inverses of differentiable functions are differentiable (see
your calculus book.)
- Functions with converging Taylor series are differentiable.
Not differentiable:
- Purely real functions such as x,
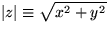 , ...
, ...
- Purely imaginary functions such as
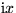 ,
, 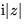 , ...
, ...
- Complex conjugates such as
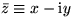 .
.
In other words, taking real or imaginary parts, absolute values,
complex conjugates, ..., all make the expression nondifferentiable.
Exercise:
Give as many 2d incompressible potential flows as you can.
You should now be able to do 18.2, 3
Next: Some Manipulations
Up: Introduction
Previous: Complex variables
![]() is the complex conjugate velocity.
is the complex conjugate velocity.
![]() is the same
whichever direction we take
is the same
whichever direction we take ![]() . In particular if we take
. In particular if we take ![]() , a change in x only, we should get the same as
when we take
, a change in x only, we should get the same as
when we take ![]() , a change in y only.
That means, if
, a change in y only.
That means, if ![]() :
:
![]()
![]()
![]()
![]()