Some Manipulations

In order to deal with complex potentials, you need to know some important facts about complex numbers:

Parts

If any complex number z is written in the form 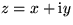where x and y are both real, then the real part of z is 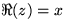. Similarly the imaginary part is 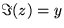. What are the real and imaginary parts of the complex streamfunction for ideal stagnation point flow, ?

Complex conjugate

To get the complex conjugate number, replace 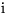everywhere by 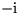. Example: :

:

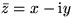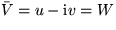What is the complex conjugate of the complex streamfunction for ideal stagnation point flow, ?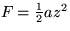

Magnitude

To get the magnitude of a complex number, multiply by the conjugate and take the square root:

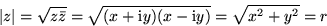
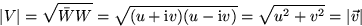
What is the magnitude of the complex streamfunction for stagnation point flow, ?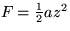

Note: z² is not a positive real number if z is complex. For complex numbers, only 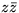is always a positive real number.

Inverse

To clean up the inverse of a complex number, try multiplying top and bottom with its complex conjugate. What is ?

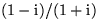Euler

An exponential with a purely imaginary argument can be written:

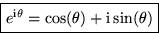
Verify this by writing out the Taylor series for the exponential.

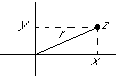
Polar form

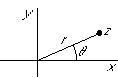
Any complex number z can be written in polar form as:

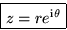
where real number r is the magnitude 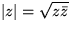of z and real number 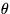is the argument 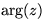of z.

Multiplication

Multiplying a complex number with a real number a magnifies the number by a: 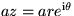. Multiplying a complex number by 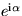rotates the number counter-clockwise over an angle : .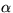

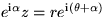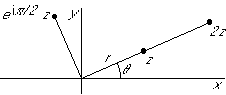
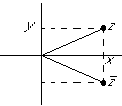
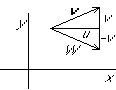
Application to finding the polar velocity components:

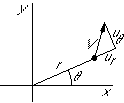
From the graph:

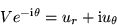
Taking the complex conjugate:

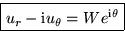
What are the polar velocity components of ideal stagnation point flow, with complex streamfunction ?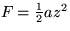

Logarithm

If 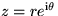is any complex number,

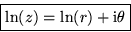
where 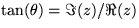. What is the logarithm of the complex streamfunction for ideal stagnation point flow, ?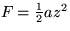

You should now be able to do 18.4