2 Reynolds Decomposition

(Panton3 26.3,4)

The Reynolds decomposition is used to analyze turbulent flows that are steady in the average. It decomposes the turbulent flow quantities in average and fluctuating components. First it defines the time averaged flow velocity (indicated with a bar above it) as

$$\fbox{$\displaystyle \overline{\vec v}\left(\vec r\right) ... ...}{T} \int_0^T \vec v\left(\vec r,t\right) \mbox{d}t\right)$}$$

The fluctuating part of the velocity can now be defined as the remainder:

$$\vec v ' = \vec v - \overline{\vec v}$$

The total velocity can then be written as

$$\vec v = \overline{\vec v} + \vec v '$$

Similarly for the pressure

$$p = \overline{p} + p'$$

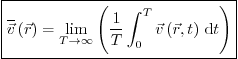
Exercise:

Sketch a velocity or pressure trace in a point in a turbulent pipe flow. In the figure, indicate what the average and fluctuating quantities are. What are the average and fluctuating velocities at the surface of the pipe? Sketch the mean (average) velocity profile in turbulent flow and in laminar flow in the same graph, assuming the two flows have the same net mass flow.

$\bullet$

Reynolds averaged equations can be found by averaging the Navier Stokes equations. In doing so, note that the average of a fluctuation (prime) quantity is always zero, and that averaging an already averaged (bar) quantity leaves the averaged quantity unchanged. Also note that averaging is a linear operation that commutes with addition and differentiation.

Continuity: Averaging the continuity equation gives

$$\overline{\frac{\partial u_i}{\partial x_i}} = 0 \quad\Lon... ...ine{ \frac{\partial \overline{u_i} + u'_i}{\partial x_i}} = 0$$

As noted above, the average has no effect on the first already averaged term, but the second fluctuating term averages to zero. So you get:

$$\fbox{$\displaystyle \frac{\partial \overline{u_i}}{\partial x_i} = 0 $}$$

This takes the form of the normal continuity equation, but applied to the average velocity.

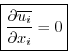
Viscous Stress Tensor: Assuming that $\mu$ is constant,

$$\overline{\tau_{ij}} = \overline{\mu \left( \frac{\parti... ...{\frac{\partial \overline{u_j} + u'_j}{\partial x_i}} \right)$$

or using the same arguments as for continuity

$$\fbox{$\displaystyle \overline{\tau_{ij}} = \mu \left( \... ..._j} + \frac{\partial \overline{u_j}}{\partial x_i} \right)$}$$

This takes the form of the normal Newtonian stress tensor, but applied to the average velocity.

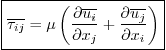
Momentum Equations: The momentum equations (Navier-Stokes equations) are in conservation form and in index notation:

$$\frac{\partial\rho u_i}{\partial t} + \frac{\partial\rho u... ...partial p}{\partial x_i} + {\partial \tau_{ij}}{\partial x_j}$$

so Reynolds averaging gives

$$\overline{ \frac{\partial\rho\left(\overline{u_i} + u'_i\r... ...frac{\partial\overline{\tau_{ij}} + \tau'_{ij}}{\partial x_j}}$$

Now note here in the second term that the average of a product of fluctuating quantities is not zero. For example, $u'_iu'_i$, a square, is obviously always positive, so its average must be positive too. Taking that into account, you get for the momentum equations:

$$\frac{\partial \rho \overline{u_i} \overline{u_j}}{\parti... ...tial x_i} + \frac{\partial\overline{\tau_{ij}}}{\partial x_j}$$

The second term above is not in the normal momentum equations, It is seen from comparing this additional term with the final term above that it acts as an additional viscous force per unit volume. In that picture,

$$\fbox{$\displaystyle \tau_{ij}^{\rm{R}} \equiv - \rho \overline{u_i' u_j'}$}$$

is the stress, called the Reynolds stress.

In those terms the momentum equations take the form:

$$\fbox{$\displaystyle \frac{\partial \rho \overline{u_i} ... ...artial\overline{\tau_{ij}}+\tau_{ij}^{\rm{R}}}{\partial x_j}$}$$

That is like the normal steady Navier Stokes equations, but for the average velocity and pressure, and including the additional Reynolds stress.

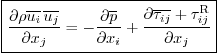
Unfortunately, the Reynolds stress is not known unless you solve the full unsteady Navier-Stokes equations. To avoid this humongous task, guessing (also known as modelling) is needed.

Exercise:

Compare the sizes of the Reynolds stress and the laminar stress in high Reynold number flows. In the turbulent pipe flow, is the Reynolds stress everywhere much larger than the laminar stress? If not, at what locations is the laminar stress larger?

$\bullet$