3 Molecular model of (laminar) viscosity

(Panton3 6.2)

$$\hbox{\epsffile{figures/molvis.ps}}$$

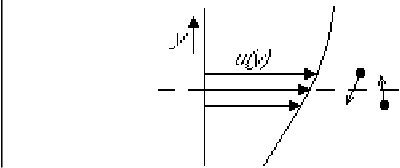
To understand the Reynolds stress more clearly, you must first understand how the normal laminar shear stress arises from molecular motion. To do so, look at the steady unidirectional laminar flow sketched in the figure above. In particular, consider the net momentum transfer due to molecular motion through the plane indicated by the broken line. Let’s assume the fluid is a gas. The molecules of the gas are always in random molecular heat motion. On average, they travel a small distance, called the “free-path length” $\lambda$, between collisions with other molecules. The velocity with which they travel between collisions is of the order of the speed of sound $a$.

Due to the random motion, there will always be molecules crossing the broken-line plane. But on average, there will be just as much molecules crossing the plane from below as there will be crossing the plane from above. So the net numbers of molecules above and below the plane do not change. That is illustrated in the figure by a pair of molecules crossing the plane from opposite sides.

Now if the velocity profile was uniform, the $x$-momentum crossing the plane from below would also cancel the $x$-momentum crossing the plane from above. So there would be no net $x$-momentum transfer through the plane either. But if the velocity profile is sloped as in the figure, the molecule coming from above comes from a region of somewhat higher average velocity. Higher by an amount of the order of $\lambda \partial u/\partial y$ in fact. Molecules like that will on average take this excess momentum out of the fluid above the broken line and dump it into the fluid below the broken line. So the fluid above the line slows down and the fluid below the line speeds up. Molecules crossing the plane from below have the same effect: they take a lack of momentum out of the lower fluid, speeding it up, and dump it in the upper fluid, slowing it down.

It is as if the lower fluid exerts a shear force on the upper fluid that slows it down, with an opposite reaction force where the upper fluid speeds up the lower fluid. How big is that shear force? Well, the mass of molecules crossing the layer from either side per unit area and unit time is of order $\rho a$. (Really less: only half of the molecules near the plane are going towards it, and only the vertical component of the random motion helps them get to the plane. But we are only ballparking things here.) The excess or lack of velocity being transfered across the plane is of order $\lambda\partial u/\partial y$. Since force is rate of momentum change, and momentum is mass times velocity, the viscous stress per unit area is therefore $\rho a\lambda\partial u/\partial y$.

That makes the kinematic viscosity $\nu$ of order $a\lambda$. You could also have concluded that from a simple dimensional analysis. But now you have the physical idea that can be extended to turbulence.

Exercise:

Compare the value of $\lambda a$ of standard air with its dynamic viscosity.

$\bullet$