4 Mixing length

(Panton3 26.4)

The mixing length idea tries to model the turbulent Reynolds stress much like the molecular motion created the laminar stress in the previous section. The random motion of coherent regions, eddies, of the turbulent fluid is assumed to be equivalent to the random motion of the molecules in the laminar case. As an equivalent to the free path length between molecular collisions, it is assumed that there is some “mixing length” $\ell$ over which the eddies exchange momentum. Fluid at a given plane originates from some transverse distance $\ell$ away, with much of its velocity difference left intact during the trip.

Assuming all of that is true, the kinematic eddy viscosity would be $\ell v'$, where $v'$ is the typical vertical velocity fluctuation. In other words, $\lambda\to\ell$ and $a\to v'$. From continuity, $u'_x + v'_y = 0$, so assuming that there is no strong directionality in eddy length scales, $v'$ is of the order $u'$. And $u'$ was estimated implicitly as $\ell \partial u/\partial y$ in the previous section, so the magnitude of that must be the estimate for the random transverse velocity $v'$. That gives a turbulent eddy viscosity

$$\fbox{$\displaystyle \nu_{\rm{T}} = \ell^2 \left\vert\frac{\partial \overline{u}}{\partial y}\right\vert$}$$

Assuming $\ell$ is a known quantity, this can be plugged into the averaged equations. Then they can be solved on some computer, since the Reynolds stresses are no longer unknowns. The estimate of $\ell$ could be the typical transverse length scale in free turbulence or the distance from the wall in a surface layer.

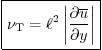
Unfortunately, many things are wrong in the story. For one, turbulent eddies are not small compared to the transverse scales of the flow, so $u'\ne\ell\partial u/\partial y$. The value of $u'$ is in fact related to the velocity at finite distances. This makes the entire idea of having universal partial differential equations (involving local derivative quantities only) unsound. (Even though many people seem to believe this fundamental problem will somehow go away if you make the local derivative terms complex enough, like in “second order modelling.”) Also, at least the larger turbulence scales are definitely directional. And the turbulent fluctuations are not independent of the mean velocity field like $a$ is.

Worse, the turbulent shear stress would always be predicted to be exactly zero at points of $\partial \overline{u}/\partial y=0$ even if there is no flow symmetry around that point, which is obviously nonsense. And surely, even if there is symmetry, the eddy viscosity should not be zero at the symmetry line. It is often a better idea to replace $\ell\vert\partial\overline{u}/\partial y\vert$ by some typical turbulent velocity. That gives a constant eddy viscosity.

Still, the mixing length idea is qualitively perhaps one of the most useful tools available because it is so simple. The more complex you make a turbulence model, the more things can go wrong. A mixing length model may be very inaccurate, but it does tend to show the correct general ideas.

Also, the mixing length idea becomes more believable if you solve the larger turbulence scales on a computer, and just model the smaller velocity fluctuations as an effective viscosity. That idea is called large eddy simulation. Even then, it is not a trivial modelling problem, unfortunately. Unlike the laminar case, there is no separation of scales between the scales you describe and the ones you model.