7 Wall-bounded flows

Channel Flow

$$\hbox{\epsffile{figures/duct.ps}}$$

A typical example of a wall-bounded flow is turbulent duct flow, as sketched above.

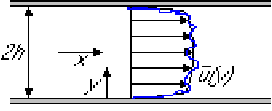
Assuming a long duct, the velocity-related quantities and the pressure gradients will be independent of $x$, just like for the laminar case. That makes turbulent duct flow simpler than turbulent boundary layers, where the streamwise gradients are smaller than the transverse ones, but not zero. Consider how the Reynolds-averaged Navier-Stokes equations simplify for the duct:

Continuity

$$\frac{\partial \overline{v}}{\partial y} = 0 \quad\Longrightarrow\quad \overline{v} = 0$$

$x$ Momentum:

$$0 = - \frac{\partial\overline{p}}{\partial x} + \frac{\par... ...^{\rm {R}} \equiv \tau_{xy}^{\rm {R}} = - \rho \overline{u'v'}$$

$y$-Momentum:

$$0 = - \frac{\partial\overline{p}}{\partial y} + \frac{\pa... ...rtial y} \qquad \tau_{yy}^{\rm {R}} = - \rho \overline{v'v'}$$

The $y$-momentum equation can easily be integrated to give

$$\fbox{$\displaystyle p + \rho\overline{v'v'} = p_w(x) $}$$

where $p_w$ is the pressure on the walls. So, unlike in laminar duct flow, the pressure is not independent of $y$; it is highest at the walls, (where $v'=0$ because of the wall boundary conditions), and lowest in the center of the duct.

If we put the above pressure into the $x$-momentum equation, noting that $\rho\overline{v'v'}$ as a velocity quantity is independent of $x$, we get:

$$\fbox{$\displaystyle \tau + \tau^{\rm{R}} = - \frac{\mbox... ...{\partial y} \quad \tau^{\rm{R}} = - \rho \overline{u'v'} $}$$

where $y$ is taken to be zero on the center line of the duct. So, the total stress, laminar plus Reynolds, is linear in $y$, and vanishes (by symmetry) on the center line.

Now a turbulent flow will dissipate much more kinetic energy than a laminar one under the same conditions. The irreversible loss of kinetic energy must come from a much larger pressure gradient pushing the flow through the duct. But since the net force on the fluid must be zero, the shear force exerted by the wall on the fluid must be much greater too. In short, in the above equation, both the pressure gradient and the net shear stress are much larger than in the laminar case.

Now at the walls, the Reynold stress $\tau^{\rm {R}}$ = $\rho\overline{u'v'}$ is zero because of the wall boundary condition on the velocity. So there must be a very large laminar stress $\tau$ at the walls. And since $\tau$ = $\mu\partial\overline{u}/\partial y$, the velocity profile must be varying extremely rapidly near the walls. But, since the profile is monotonous to the center, this can only be true in a thin layer, called the surface layer, at each of the two walls. Outside these layers, the Reynolds stress must dominate and the laminar stress can be ignored.

Exercise:

Sketch the velocity profiles for laminar and turbulent flow with the same mass flow through the duct. Indicate the layer near the wall and how it is different from the laminar flow case.

$\bullet$

By convention, the magnitude of the shear stress at the wall is written in terms of a ``friction velocity'' $u^*$:

$$\fbox{$\displaystyle \tau_0 = - h \frac{\mbox{d}p_w}{\mbox{d}x} \equiv \rho {u^*}^2$}$$

It is a measure of how much stress the overall flow exerts on the fluid near the wall.

It seems reasonable to assume that in the thin surface layers, the large-scale features of the flow are only evident through the stress they impose, as measured by $u^*$. So if we take $\Delta y$ to be the distance from the wall, we can assume that

$$\overline{u} = f_0(\Delta y,u^*,\nu)$$

Then dimensional analysis gives the ``law of the wall'':

$$\fbox{$\displaystyle \frac{\overline{u}}{u^*} = f\left(\frac{u^*\Delta y}{\nu}\right)$}$$

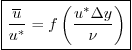
This says that in the surface layer, the nondimensional flow depends only on an effective Reynolds number formed with the distance from the wall. This Reynolds number decreases to zero when approaching the wall. In fact, close to the wall there is a sublayer in which the Reynolds number becomes too low for turbulence to sustain itself. This sublayer is called the viscous sublayer.

In the center region of the duct, in between the two surface layers, the picture to keep in mind is that the strong turbulent mixing would create a uniform velocity profile if there were no walls. However, the surface layers exert a shear force, measured by $u^*$, on the edges of the center region, preventing the uniform profile to fully develop. It seems reasonable then to assume that the deviation from a uniform profile is functionally given by

$$\overline{u} - u_{\mbox{max}} = F_0(y,h,u^*)$$

Dimensional analysis then produces the so-called ``velocity defect law'':

$$\fbox{$\displaystyle \frac{\overline{u} - u_{\mbox{max}}}{u^*} = F\left(\frac{y}{h}\right)$}$$

Now consider some hypothetical thin layer, close to the bottom wall, but still well above the still thinner surface layer. In such a layer, both the law of the wall (for $\Delta yu^*/\nu$ relatively large) and the velocity defect law (for $y\approx-h$) must be valid. Such a layer, in which two different expressions are both valid, is called a matching layer. For turbulent boundary layers, the matching region is referred to as the inertial sublayer. (But “inertial region” would have been a more accurate name since a matching region has no clearly defined boundaries. Note also that by definition the inertial sublayer has to be thick compared to the surface layer below it and thin compared to the duct size.)

If both the law of the wall and the velocity defect law must be valid in the inertial sublayer, then their $y$ derivatives must match too. Writing that out gives:

$$\frac{y}{u^*} \frac{\mbox{d}u}{\mbox{d}y} = f'\left(\frac{... ...t) \frac{y u^*}{\nu} = F'\left(\frac{y}{h}\right) \frac{y}{h}$$

And if two functions of different arguments must be the same, then each must be a constant. (Otherwise you could simply change just one of the arguments to create inequality.) So the two expressions above must be a constant. This constant is normally indicated as $1/\kappa$, where $\kappa$ is called the “von Kármán’s” constant. Its value is often quoted as 0.4, but it might be somewhat less, like 0.33, at high enough Reynolds numbers.

The two expressions above can now be integrated to give the shape of the velocity profile in the inertial sublayer:

$$\fbox{$\displaystyle \frac{\overline{u}}{u^*} = \frac1\kap... ...right) + C_f \qquad \left(\frac{y u^*}{\nu}\to\infty\right)$}$$

$$\fbox{$\displaystyle \frac{\overline{u} - u_{\mbox{max}}}{... ...ac{y}{h}\right) + C_F \qquad \left(\frac{y}{h} \to 0\right)$}$$

The derivation of this logarithmic profile by Millikan in 1939 was one of the landmark events in turbulence theory.

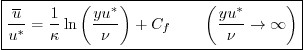
Substracting the two equations above, we get the ``logarithmic friction law'':

$$\fbox{$\displaystyle \frac{u_{\mbox{max}}}{u^*} = \frac 1\kappa \ln\left(\frac{h u^*}{\nu}\right) + C$}$$

Recall that $u^*$ is really a measure of the wall shear, or equivalently the pressure gradient needed to keep the flow moving. So the above equation relates the pressure gradient needed to drive the flow to the maximum velocity in the duct.

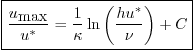
Exercise:

Discuss figure 26.13 and how it verifies and does not verify the above discussion for the case of a boundary layer.

$\bullet$