Substitute the Eulerian velocity field of stagnation point flow
into the (Eulerian) Euler equations. In the force per unit volume,
include the gravity force per unit volume. Assume that gravity is
in the minus 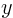 -direction. You get three equations for the
pressure, one giving its
-direction. You get three equations for the
pressure, one giving its 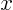 -derivative, one its
-derivative, one its 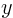 derivative, and
the third its
derivative, and
the third its 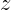 -derivative. More than one equation for a single
scalar unknown
-derivative. More than one equation for a single
scalar unknown 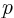 is usually too much, but show that in this case,
there is indeed a solution
is usually too much, but show that in this case,
there is indeed a solution 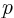 that satisfies all three equations.
Find out what it is. Does it satisfy the Bernoulli law?
that satisfies all three equations.
Find out what it is. Does it satisfy the Bernoulli law?
Note: to find the pressure correctly, solve the Euler equation in
the 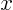 -direction for the pressure. The integration constant will
depend on
-direction for the pressure. The integration constant will
depend on 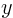 and
and 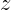 . Substitute this result into the Euler
equation in the
. Substitute this result into the Euler
equation in the 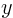 -direction to narrow down the integration
constant. Then substitute this result into the Euler equation in
the
-direction to narrow down the integration
constant. Then substitute this result into the Euler equation in
the 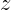 -direction to narrow down the constant even more.
-direction to narrow down the constant even more.
![]() -direction for the pressure. The integration constant will
depend on
-direction for the pressure. The integration constant will
depend on ![]() and
and ![]() . Substitute this result into the Euler
equation in the
. Substitute this result into the Euler
equation in the ![]() -direction to narrow down the integration
constant. Then substitute this result into the Euler equation in
the
-direction to narrow down the integration
constant. Then substitute this result into the Euler equation in
the ![]() -direction to narrow down the constant even more.
-direction to narrow down the constant even more.