3 9/19 W

1. In Poiseuille flow (laminar flow through a pipe), the velocity field is in cylindrical coordinates given by
   
   $$\vec v = {\widehat \imath}_z v_{\rm max} \left(1 -\frac{r^2}{R^2}\right)$$
   
   
   where $v_{\rm {max}}$ is the velocity on the centerline of the pipe and $R$ the pipe radius. (a) Use Appendices B and C to find the velocity gradient and strain rate tensors of this flow. Do not guess. (b) Evaluate the strain rate tensor at $r=0$, $\frac12R$ and $R$. What can you say about the straining of small fluid particles on the axis? (c) Is Poisseuille flow an incompressible flow? (d) Also find the vorticity. Do particles on the axis rotate? If not, what do they do?

2. (20pt) For the Poisseuille flow of the previous question, derive the principal strain rates and the principal strain directions for an arbitrary radial position $r$ using class procedure.

3. Make a neat picture of a vertical $r,z$ plane through the axis showing, for a point at an arbitrary $r,z$, a small cubic fluid particle, in cross section, that is aligned with the principal strains at that point. Using arrows as appropriate, show the translational, straining, and average rotational motions that this particle is performing. If the particle was a small solid sphere, instead, would you expect it to rotate, and if so, in which direction?

4. Write out the continuity equation
   
   $$\frac{1}{\rho} \frac{{\rm D}\rho}{{\rm D}t} + {\rm div}\vec v = 0$$
   
   
   in cylindrical and spherical coordinates, for both a compressible and an incompressible fluid. (Here incompressible means that the density of individual fluid particles is constant, not that all fluid particles must have the same density. Usually, when people say incompressible they mean that the density is the same everywhere. But looking in the sea, different regions have different density, because of different salt, but the individual particles are still pretty much incompressible.) Note that
   
   $$\frac{\rm D}{{\rm D}t} = \frac{\partial}{\partial t} + \vec v \cdot \nabla$$
   
   
   and use the appendices.

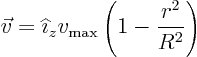
   Next assume that $\vec v$ and $\rho$ only depend on $r$ and $t$ (so the flow is cylindrically or spherically symmetric). How do the equations simplify? In the incompressible case, you should see that there is a quantity that must be a constant (at least for any given time) in each flow. What is it? In the compressible steady flows, there is also a quantity that must be constant. What is that? What happens to the radial velocity when going to large $r$?

5. Use the expression derived in class to ballpark the kinematic viscosity $\nu$ of standard air. From that ballpark the kinematic viscosity $\mu$. Use the data from Appendix A in the book and the posted solutions of homework 1 for the free path length. Compare with the exact values.

6. Two-dimensional Poiseuille flow (in a duct instead of a pipe) has the velocity field
   
   $$\vec v = {\widehat \imath}v_{\rm max} \left(1-\frac{y^2}{h^2}\right)$$
   
   
   Here $x$ is along the centerline of the duct, $y$ across the gap measured from the middle, and $h$ is half the duct height. Neatly sketch the duct and its velocity profile. Find the viscous stress tensor for this flow, assuming a Newtonian fluid, using Table C3 in the book. Evaluate the viscous stress tensor at $y/h=\frac12$. Draw a little cube of fluid at that position in the duct (in cross-section), and sketch all viscous stresses acting on that cube. In a different color, also sketch the inviscid pressure forces acting on it. (assume the pressure has some value $p$.)

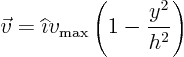
   Next assume that the little cube is rotated counter-clockwise over a 30 degree angle (around the $z$-axis). Find the total stresses $\sigma$ (including pressure) normal and $\tau$ tangential on the now oblique front surface of the little cube. To do so, first find a unit vector $\vec n$ normal to the surface. Then find the vector stress on the surface using $\vec R=\bar{\bar\tau}\vec n$. Then find the components of $\vec R$ in the direction of $\vec n$ (so normal to the surface), and normal to $\vec n$ (so tangential to the surface).

   Note: This is essentially question 5.3 from the book, but do not assume that the pressure is 5; just leave it as $p$.