3 9/18 W

1. In Poiseuille flow (laminar flow through a pipe), the velocity field is in cylindrical coordinates given by
   
   $$\vec v = {\widehat \imath}_z v_{\rm max} \left(1 -\frac{r^2}{R^2}\right)$$
   
   
   where $v_{\rm {max}}$ is the velocity on the centerline of the pipe and $R$ the pipe radius. (a) Use appendix B to determine whether this is an incompressible flow. (b) Use Appendices B and C to find the velocity gradient and strain rate tensors of this flow. Do not guess. Compare whether the results are consistent. (c) Evaluate the strain rate tensor at $r=0$, $\frac12R$ and $R$. What can you say about the straining of small fluid particles on the axis? (d) Also find the vorticity. Do particles on the axis rotate? If not, what do they do?

2. (20pt) For the Poisseuille flow of the previous question, derive the principal strain rates and the principal strain directions for an arbitrary radial position $r$ using class procedure.

3. For the Poisseuille flow of the previous questions, make a neat picture of a vertical $r,z$ plane through the axis showing, for a point at an arbitrary $r,z$, a small cubic fluid particle, in cross section (so a square), that is aligned with the principal strains at that point. Using arrows as appropriate, show the translational, straining, and average rotational motions that this particle is performing. If the particle was a small solid sphere, instead, would you expect it to rotate, and if so, in which direction?

4. Write out the continuity equation
   
   $$\frac{1}{\rho} \frac{{\rm D}\rho}{{\rm D}t} + {\rm div}\vec v = 0$$
   
   
   in cylindrical and spherical Eulerian coordinates, for both a compressible and an incompressible fluid separately (4 equations).

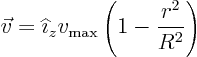
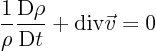
   (Here incompressible means that the density of individual fluid particles is constant, not that all fluid particles must have the same density. Usually, when people say incompressible they mean that the density is the same everywhere. But looking in the sea, different regions have different density, because of different salt, but the individual particles are still pretty much incompressible.)

   Note that
   

   $$\frac{\rm D}{{\rm D}t} = \frac{\partial}{\partial t} + \vec v \cdot \nabla$$
   
   
   and use the appendices.

   Next assume that $\vec v$ and $\rho$ only depend on $r$ and $t$ (so the flow is cylindrically or spherically symmetric). How do the equations simplify?

   In the incompressible case (density the same everywhere), you should see that there is a quantity that must be a constant (at least for any given time) in each flow. What is it?

   In the compressible steady flows, there is also a quantity that must be constant. What is that? What happens to the radial velocity when going to large $r$?

5. Use the expression derived in class to ballpark the kinematic viscosity $\nu$ of standard air. From that ballpark the dynamic viscosity $\mu$. Use the data from Appendix A in the book and the posted solutions of homework 1 for the free path length. Compare with the exact values.