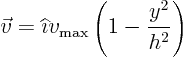|
|
|
|
Next: 5 10/02 W |
|
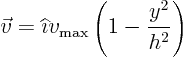
Evaluate the viscous stress tensor at ![]() . Draw a little
cube of fluid at that position in the duct (in cross-section, and
aligned with the axis), and sketch all viscous stresses acting on
that cube. In a different color, also sketch the inviscid pressure
forces acting on it. (Assume the pressure has some value
. Draw a little
cube of fluid at that position in the duct (in cross-section, and
aligned with the axis), and sketch all viscous stresses acting on
that cube. In a different color, also sketch the inviscid pressure
forces acting on it. (Assume the pressure has some value ![]() .)
.)
Next assume that the little cube is rotated counter-clockwise over a
30 degree angle (around the ![]() -axis). Find the total stresses
-axis). Find the total stresses
![]() (including pressure) normal and
(including pressure) normal and ![]() tangential on the
now oblique front surface of the little cube. To do so, first find
a unit vector
tangential on the
now oblique front surface of the little cube. To do so, first find
a unit vector ![]() normal to the surface. Then find the vector
stress on the surface using
normal to the surface. Then find the vector
stress on the surface using ![]() . Then
find the components of
. Then
find the components of ![]() in the direction of
in the direction of ![]() (so
normal to the surface), and normal to
(so
normal to the surface), and normal to ![]() (so tangential to the
surface).
(so tangential to the
surface).
Note: This is essentially question 5.3 from the book, but do
not assume that the pressure is 5; just leave it as ![]() .
.