Write down the worked-out mathematical expressions for the
integrals requested in question 5.1. This is a good exercise in
identifying various surface and volume integrals in integral
conservation laws. Explain their physical meaning, if any. Don't
worry about actually doing the integrations. However, show
integrands and limits completely worked out.
Take the surfaces 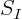 ,
, 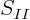 ,
, 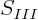 , and
, and 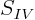 to be
one unit length in the
to be
one unit length in the 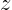 -direction. (To figure out the correct
direction of the normal vector
-direction. (To figure out the correct
direction of the normal vector 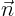 at a given surface point,
note that the control volume in this case is the right half of the
region in between two cylinders of radii
at a given surface point,
note that the control volume in this case is the right half of the
region in between two cylinders of radii 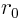 and
and 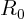 and of unit
length in the
and of unit
length in the 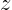 -direction. The vector
-direction. The vector 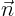 is a unit normal
vector sticking out of this control volume.)
is a unit normal
vector sticking out of this control volume.)
![]() ,
, ![]() ,
, ![]() , and
, and ![]() to be
one unit length in the
to be
one unit length in the ![]() -direction. (To figure out the correct
direction of the normal vector
-direction. (To figure out the correct
direction of the normal vector ![]() at a given surface point,
note that the control volume in this case is the right half of the
region in between two cylinders of radii
at a given surface point,
note that the control volume in this case is the right half of the
region in between two cylinders of radii ![]() and
and ![]() and of unit
length in the
and of unit
length in the ![]() -direction. The vector
-direction. The vector ![]() is a unit normal
vector sticking out of this control volume.)
is a unit normal
vector sticking out of this control volume.)