


Next: Basic Laws
Up: Notes on the Panton
Previous: Vector Calculus and Index
Subsections
Before we can try to find out how complete flow fields look, we first
need to understand how small regions of fluid behave. In particular,
how their motion consists of both rotation and deformation processes.
We also want to understand quantities such as particle paths and
streamlines that are frequently used to examine experimental or
computed flow fields.
- Ability to define the vocabulary
- Can find streamlines and particle paths
- Can find vorticity in any standard coordinate system.
- Can find moving time derivatives.
- Can identify the strain-rate tensor.
- Can find circulation by direct integration.
- Lagrangian
- Eulerian
- Ideal stagnation point flow.
- Particle path.
- Streamline.
- Steady flow
- Lagrangian derivative.
- Vorticity.
- Rate-of-strain tensor.
For the linear shear flow of section 4.4,
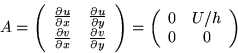
Hence, averaging A and its transpose, the strain rate matrix is
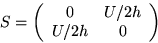
with eigenvalues (principal strain rates) 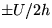 and corresponding
eigenvectors
and corresponding
eigenvectors 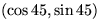 and
and 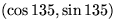 . So the
principal axes are under 45 degrees with the plates and flow direction.
. So the
principal axes are under 45 degrees with the plates and flow direction.
The only nonzero vorticity component is in the z-direction:
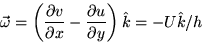



Next: Basic Laws
Up: Notes on the Panton
Previous: Vector Calculus and Index
Author: Leon van Dommelen
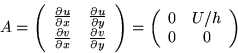
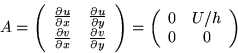
![]()
![]()