Simplified Description

Let's restrict attention to the specific problem of adding heat to a flow in a constant area duct. In that case, it is the value of H at the exit that we modify by adding heat. Let us examine when we get into trouble doing so.

To simplify, we will first create a single equation in the single unknown like we did in the hand-out on normal shocks: we solve (1) for and substitute that into (2) and (3) to eliminate u from those equations:

To make it even simpler, let's assume, (for this simplified example only,) that we are dealing with a perfect gas, for which . Then, if we solve (2') for and put it into (3'), we get

The first term in the right hand side dominates for large and the second for small , so the net graph of H versus looks like shown below:

There is a maximum for H for a special value of that we will indicate by .

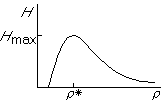
Now in the next figure we show what happens if, starting from an arbitrary starting flow that we have indicated by a dot, we change the value of H an infinitesimal amount :

This changes the value of the flow density by a corresponding amount . In terms of linear algebra, the ``linearized problem'' , where f' is the derivative of the function (4), has a unique solution .

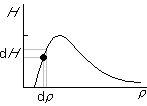
But clearly, there will be a problem when the initial state is at the maximum of the curve, because there the derivative f'=0, and we would be dividing by 0. In fact, there is really no solution if we try to raise H any more:

The flow is ``choked'' at the maximum of the curve. In terms of linear algebra, the linearized problem has no solutions when is nonzero, and infinitely many when it is.

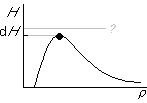
Now let's consider shocks. The two sides of a shock have the same total enthalpy H, so the two sides of an arbitrary shock show up in the graph as shown by the two dots:

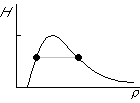
Remember that a weak shock is one in which the flow quantities, including , barely change across the shock. From the figure, it is clear that weak shocks must therefor be right at the maximum of the curve:

So the existence of weak shocks is exactly the condition of being at the top of the curve and in trouble. And we found that to be true when Mach equals one. In fact we defined the speed of sound that way.

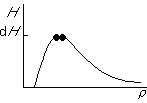
Also notes that since the Mach number crosses one at the maximum, and one side of an arbitrary shock is located before the maximum and the other side after it, one side of a shock will be supersonic, and one side subsonic. That is something that we proved earlier for perfect gases from the Prandtl relationship. Here we see it applies generally.

That summarizes how it all hangs together. In the next section we will do the full problem of three equations in three unknowns and an arbitrary gas.